Basen
Im Sinne einer kleinen Vorbereitung auf die nächsten Themen betrachten wir diese Woche einige Begriffe der linearen Algebra (LinAlg).
Basen
Dazu betrachten wir drei Bereiche
- Polynome $p_n$
- Trigonometrische Polynome $T_n$
- Reelle Vektorräume $R^n$
Aufgabe
- Bei allen dreien kommt der Parameter $n$ vor. Was könnte $n$ bedeuten?
- Wie sieht ein allgemeines Element aus diesen drei Bereichen aus?
Aufgabe
- Aus welchen Grundbausteinen werden diese Elemente zusammengesetzt?
- Welche mathematischen Operationen werden dafür gebraucht?
Polynombasis
Ein Polynom vom Grad $n$ in der Variable $x$ hat die Grundform $p_n(x)=\sum_{i=0}^n a_i\cdot x^i$ und damit die Basiselemente $$1,\; x,\; x^2,\; \dots,\; x^n $$ Alle diese Elemente als Menge bilden die Basis von $p_n$.
Basis eines trigonometrischen Polynoms
Ein trigonometrisches Polynom vom Grad $n$ in der Variablen $x$ hat die Grundform $T_n(x)=\sum_{i=0}^n a_i\cdot \cos (ix) + b_i \cdot \sin (ix)$ und damit die Basiselemente $$1,\; \cos(x),\; \sin(x),\; \cos(2x),\; \sin(2x),\; \dots ,\; \cos(nx),\; \sin(nx)$$
Die Ebene ($\mathbb{R}^2$) und der Raum ($\mathbb{R}^3$)
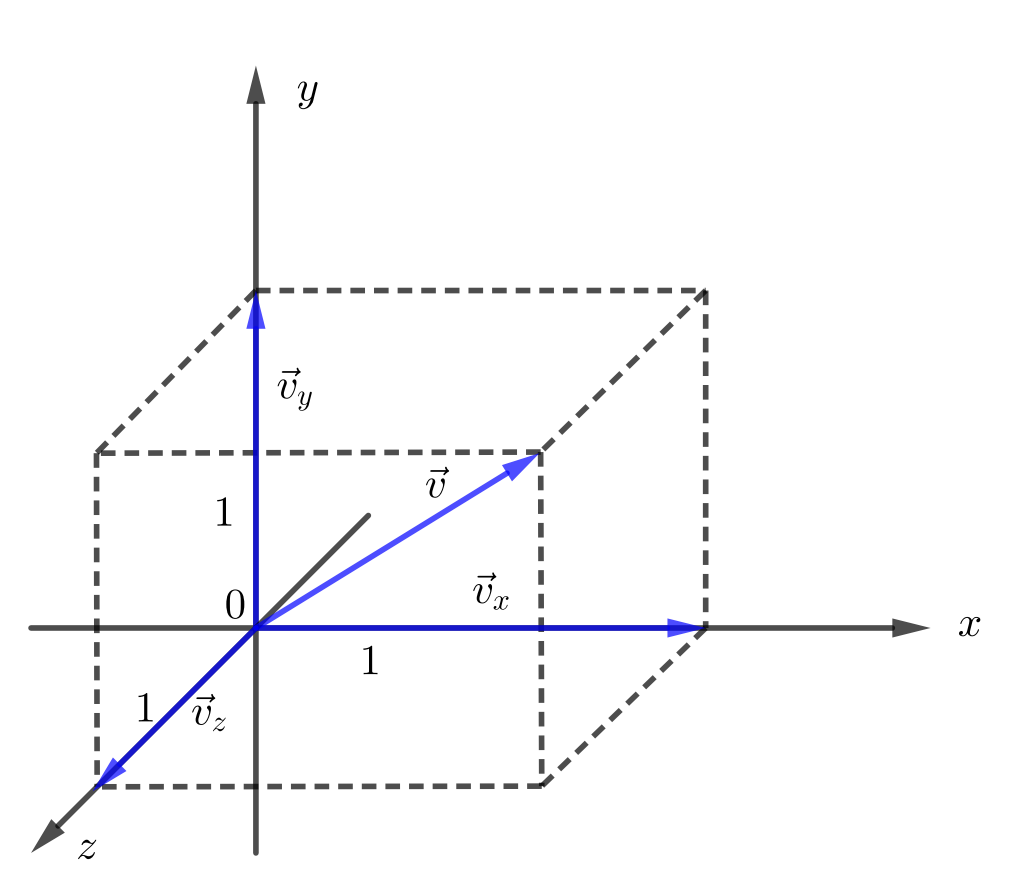
Als nächstes folgt die Darstellung von Vektoren mit einem Koordinatensystem in der Ebene ($\mathbb{R}^2$) und im Raum ($\mathbb{R}^3$). Dazu verwenden wir ein kartesisches Koordinatensystem.
Jeder Vektor $\vec{v}$ wird als Summe der Richtungsvektoren (entlang der Koordinatenachsen) $\vec{v}_x$, $\vec{v}_x$ und $\vec{v}_z$ aufgefasst. D.h. $$\vec{v}=\vec{v}_x + \vec{v}_y + \vec{v}_z $$ Die Richtungsvektoren sind wiederum skalare Vielfache der Einheitsvektoren $\vec{e}_x$, $\vec{e}_y$ und $\vec{e}_z$. Diese Einheitsvektoren (auch Basisvektoren genannt) haben die Länge 1 und die Richtung der entsprechenden Koordinatenachsen. $$\vec{v}_x=v_x\cdot \vec{e}_x, \quad \vec{v}_y=v_y\cdot \vec{e}_y, \quad\vec{v}_z=v_z\cdot \vec{e}_z$$ Jeder Vektor $\vec{v}$ lässt sich wie folgt aufschreiben. $$ \vec{v}=\vec{v}_x + \vec{v}_y + \vec{v}_z =v_x\cdot \vec{e}_x + v_y\cdot \vec{e}_y + v_z\cdot \vec{e}_z$$ Mit der Konvention in der Ebene$$\vec{e}_x=\left( \begin{array}{c} 1\\0 \end{array} \right),\quad \vec{e}_y=\left( \begin{array}{c} 0\\1 \end{array} \right) $$ und im Raum $$\vec{e}_x=\left( \begin{array}{c} 1\\0\\0 \end{array} \right),\quad \vec{e}_y=\left( \begin{array}{c} 0\\1\\0 \end{array} \right),\quad \vec{e}_z=\left( \begin{array}{c} 0\\0\\1 \end{array} \right) $$ergibt sich folgende Darstellung eines Vektors mit kartesischen Koordinaten. $$\vec{v}=v_x\cdot \vec{e}_x + v_y\cdot \vec{e}_y = v_x\cdot \left( \begin{array}{c} 1\\0 \end{array} \right) + v_y\cdot \left( \begin{array}{c} 0\\1 \end{array} \right) = \left( \begin{array}{c} v_x\\0 \end{array} \right) + \left( \begin{array}{c} 0\\v_y \end{array} \right) = \left( \begin{array}{c} v_x\\v_y \end{array} \right)$$
$$\vec{v}=v_x\cdot \vec{e}_x + v_y\cdot \vec{e}_y + v_z\cdot \vec{e}_z = v_x\cdot \left( \begin{array}{c} 1\\0\\0 \end{array} \right) + v_y\cdot \left( \begin{array}{c} 0\\1\\0 \end{array} \right) + v_z\cdot \left( \begin{array}{c} 0\\0\\1 \end{array} \right) = \left( \begin{array}{c} v_x\\v_y\\v_z \end{array} \right)$$ Abschliessend noch drei Bezeichnungen:
- Die Zahlen $v_x$, $v_y$ und $v_z$ heissen die Koordinaten des Vektors $\vec{v}$.
- Die Vektoren $\vec{v}_x$, $\vec{v}_y$ und $\vec{v}_z$ heissen die Komponenten des Vektors $\vec{v}$.
- Die Vektoren $\vec{e}_x$, $\vec{e}_y$ und $\vec{e}_z$ heissen die kanonischen Basisvektoren und bilden eine Basis des $\mathbb{R}^3$.
Aufgabe
- Gibt es mehr als eine Basis für den Raum, oder die Ebene?
- Finde zwei weitere Basen des $\mathbb{R}^3$.
Orthogonale Basen
Sind die Basisvektoren paarweise senkrecht zueinander, dann sprechen wir von einer orthogonalen Basis. Orthogonal bedeutet: $$\vec{a}\cdot \vec{b}=0$$
Aufgabe
- Konstruiere eine eigene orthogonale Basis des $\mathbb{R}^3$.
Sind die Beträge der Basisvektoren eins, so sprechen wir von einer normierten Basis. Orthogonal und normiert zusammen führt zum Begriff der Orthonormalbasis.
Aufgabe
- Konstruiere eine eigene Orthonormalbasis des $\mathbb{R}^3$.
Orthogonale Projektion
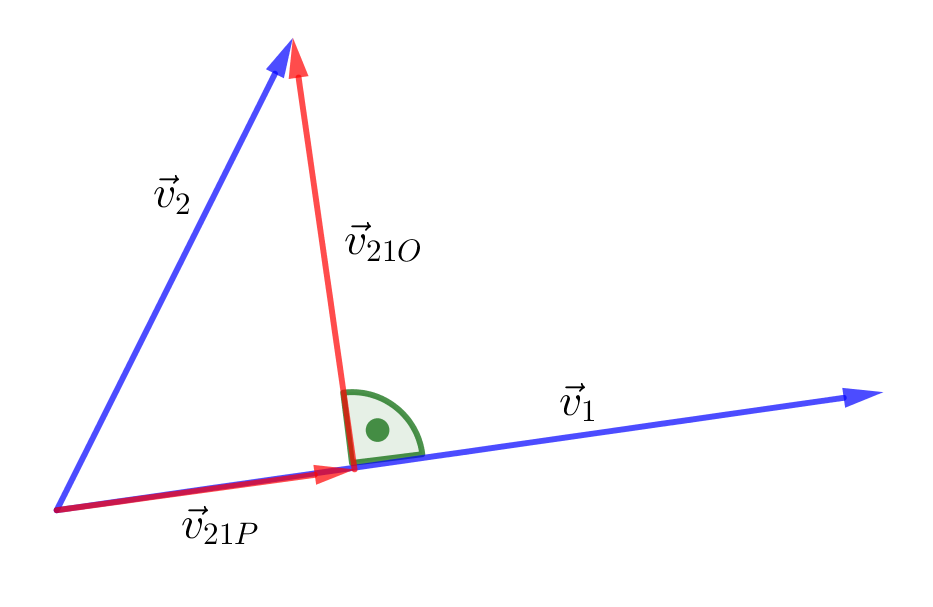
Gegeben sind die beiden Vektoren $\vec{v}_1$ und $\vec{v}_2$. Gesucht ist der Anteil von $\vec{v}_2$, welcher orthogonal zu $\vec{v}_1$ verläuft.
Dazu bestimmen wir den Anteil von $\vec{v}_2$ in Richtung von $\vec{v}_1$ und subtrahieren diesen von $\vec{v}_2$. Es gilt: $$\vec{v}_{21P}=\alpha \cdot \vec{v}_1 \qquad \text{und} \qquad \vec{v}_{21O}=\vec{v}_2-\vec{v}_{21P}$$ Wegen der Orthogonalität gilt weiter $$\vec{v}_{21O}\cdot \vec{v}_1 =0 $$ setzen wir ein erhalten wir $$\left( \vec{v}_2-\alpha \cdot \vec{v}_1 \right) \cdot \vec{v}_1 =0 $$ Damit gilt für $\alpha$ $$\alpha = \frac{\vec{v}_1 \cdot \vec{v}_2}{\vec{v}_1 \cdot \vec{v}_1}= \frac{\vec{v}_1 \cdot \vec{v}_2}{|\vec{v}_1|^2}$$ und damit gilt für $\vec{v}_{21O}$ $$\vec{v}_{21O}=\vec{v}_{2} - \frac{\vec{v}_1 \cdot \vec{v}_2}{|\vec{v}_1|^2} \cdot \vec{v}_1$$
Orthogonale Basis
Seien die Vektoren $\vec{a},\; \vec{b},\; \vec{c}, \; \vec{d}$ eine Basis des $\mathbb{R}^4$. Dann können wir schrittweise durch orthogonale Projektion eine Orthogonalbasis berechnen.
- $\vec{a}$ bleibt
- $$\vec{b'}=\vec{b}-\frac{\vec{a}\cdot\vec{b}}{|\vec{a}|^2} \cdot \vec{a}$$
- $$\vec{c'}=\vec{c}-\frac{\vec{a}\cdot\vec{c}}{|\vec{a}|^2} \cdot \vec{a} - \frac{\vec{b'}\cdot\vec{c}}{|\vec{b'}|^2} \cdot \vec{b'}$$
- $$\vec{d'}=\vec{d}-\frac{\vec{a}\cdot\vec{d}}{|\vec{a}|^2} \cdot \vec{a} - \frac{\vec{b'}\cdot\vec{d}}{|\vec{b'}|^2} \cdot \vec{b'} - \frac{\vec{c'}\cdot\vec{d}}{|\vec{c'}|^2} \cdot \vec{c'}$$
- allgemein: $$\vec{v}'_i=\vec{v}_i- \sum_{k=1}^{i-1}\frac{\vec{v}_k\cdot\vec{v}_i}{|\vec{v}_k|^2} \cdot \vec{v}_k, \quad \text{für }i\in\{2,3,\dots,n\}$$
- bleibt noch die Normierung mit $$\vec{e}_a=\frac{1}{|\vec{a}|}\cdot \vec{a} $$
Aufgabe
Implementiere obigen Algorithmus in Python für eine Basis vom $\mathbb{R}^3$ und $\mathbb{R}^4$.