• Jede/r kennt was ein Regressions-/Klassifikationsproblem ist
• Jede/r kann eine lineare Regression in Python und mit SciKit durchführen.
• Jede/r kennt die Begriffe Residuum, Residual Sum of Squares, feature space.

• Vorstellung
• Kenntniserhebung
  • Python
  • Pythonumgebung
  • Mathematik: Stochastik, Erwartungswert, Regression
• Einstieg
  • Clearview
    • New York Times Artikel
    • NZZ am Sontag Artikel oder PDF
    • NZZ Artikel oder PDF
  • Slaugherbots
• Aufgaben / Besprechung

Die meisten Probleme der Thematik maschinelles lernen («machine learning») oder künstlicher Intelligenz («artificial intelligence») lassen sich auf entweder

• Klassifikationsprobleme, oder
• Regressionsprobleme

zurückführen. Im EF Computergrafik sprechen wir mehrheitlich von «machine learning». Dieser Begriff ist enger abgegrenzt und trifft genauer, was wir machen. «machine learning» ist eine Teildisziplin von «artificial intelligence». Im Verlaufe des Kurses werden wir noch neuronale Netzwerke besprechen. Wir kommen dann noch darauf, was unter Deep Learning zu verstehen ist.

Wer die Thematik weiterverfolgen möchte, kann sich an diesen drei Büchern unten orientieren

• Elements of Statistical Learning. Knappe und konzise Einführung ist die klassischen Maschinen-Lernen-Techniken.
• Deep Learning. Vertiefung der Machinen-Lernen-Techniken vor allem für neuronale Netzwerke und «deep learning».
• Rebooting AI. Weitere Sicht in einem breiteren gesellschaftlichen Rahmen auf Probleme und Herausforderungen aktueller AI Thematiken.

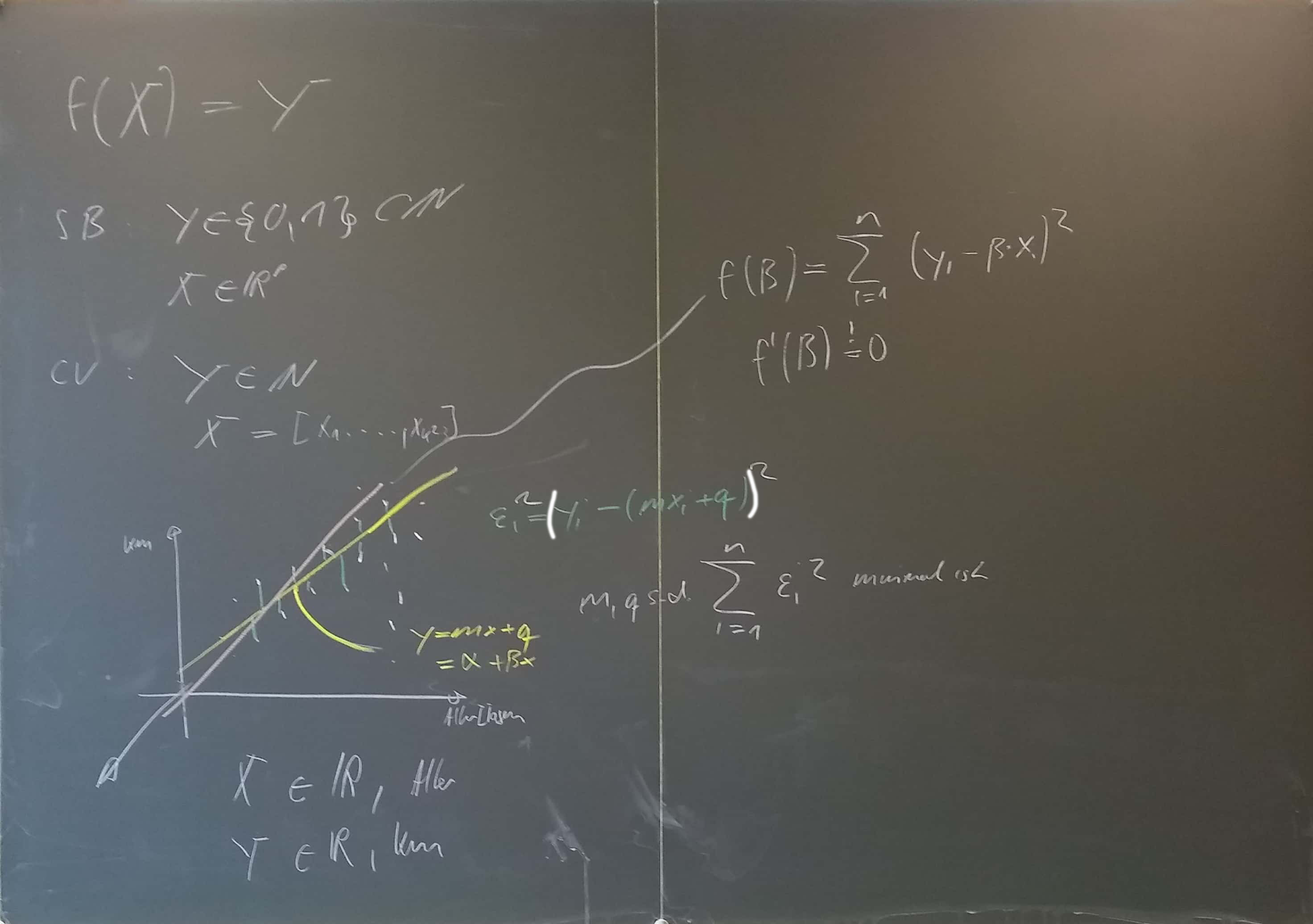
Mathematisch kann die Problematik auf folgende Gleichung heruntergebrochen werden: \[ f(X)=Y. \] $X\in\mathbb{R}^p$ ist ein Vektor. Die Menge $\mathbb{R}^p$ ist dabei der sogenannte «feature space». Dieser Vektor enthält Werte, welchen diesen Datenpunkt $X$ beschreiben. Der feature space kann grundsätzlich beliebig gross sein und sich auf auch Teilmengen von $\mathbb{R}$, z.B. $\mathbb{N}$ beschränken. Die Menge, in welchem die Werte von $Y$ liegen, wird mit $\mathcal Y$ bezeichnet.

Man unterscheidet dabei zwischen

• Regression: Ist $\mathcal Y\subset \mathbb R$, dann ist es Regressionsproblem.
• Klassifikation: Ist $\mathcal Y\subset \mathbb N$, dann ist es Klassifikationssproblem.

Die Probleme dabei, lassen sich wie folgt zusammenfassen

1. Wie finde ich ein «gutes $f$»?
2. Was ist «gut» in diesem Zusammenhang?

Die Antwort auf die erste Frage, sind verschiedene Methoden. Im EF werden wir voraussichtlich folgende Methoden vertieft kennenlernen:

• Regression (Uni- und multivariat) als Brückenschlag zur normalen Mathe
• Smoothing-Splines als Brückenschlag zu Teil II
• $k$-nearest-neighbours als erste echte nicht-lineare Variante
• Neuronale Netze

Dass $X$ und $Y$ gross geschrieben werden, hat damit zu tun, dass beide als Zuvallsvektoren verstanden werden. Zufallsvektoren sind Vektoren, welche aus Zufallsvariablen (Zufallsgrössen) bestehen. So ist $X=[X_1,X_2,\ldots,X_p]'$ ein $p$-Dimensionaler Zufallsvektor. $Y$ ist üblicherweise $1$-dimensional.

Grundsätzlich ist immer die Idee, dass mein Modell $f$ möglichst genau den Wert der Variable $Y$ vorhersagt, wenn ich die zugehörigen Werte von $X$ kenne. Im Regressionskontext ist dies häufig, die mittlere quadratische Abweichung (residual sum of squares, RSS).

Gehen wir davon aus, dass wir $n$ Beobachtungen ($=$ Datenpunkte $\neq$ Zufallsvariable) $x_i=[x^1,x^2,\ldots,x^p]$ und zugehörige Werte $y_i$ haben.¹⁾ Man definiert dann \[ \text{RSS}(f)=\sum_{i=1}^n (f(x_i)-y_i)^2. \] Im einfachsten Fall suchen wir ein lineares $f$: Gehen wir von $x_i=[x^1]$ aus und einer linearen Funktion aus. Damit setzten wir voraus, dass $Y_i=\alpha+\beta X_i+\varepsilon_i$ ist. $\varepsilon_i$ ist dabei ein Fehlerterm, der die Ungenauigkeit des Modells «auffängt». Man nennt entsprechend $y_i-(\alpha+\beta x_i)$ auch das Residuum eines Datenpaares $(x_i,y_i)$.

Hat man die bekannten Grössen $x_i$ so kann man die Vorhersage $f(x_i)=\hat y_i$ berechnen (predicted value; prediction). Das Residuum ist dann einfach $\hat y_i-y_i$.

1. Welches sind Klassifizierungsaufgaben bei Clearview? Was ist der Feature Space? Was ist $|\mathcal{Y}|$?
2. Welches sind Klassifzierungsaufgaben beim Slaugherbots? Wie viele Elemente hat die Menge $\mathcal Y$?

Verwende für die nachfolgenden Aufgaben den folgenden Datensatz Auto Daten. Schaue dir zuerst den Datensatz in einem Texteditor an, die Datei fields.txt enthält die Spaltennamen. Verwende für Aufgabe 1 als abhängige Variable $y$ die gefahrenen Kilometern, als unabhängige Grösse $X$ das Alter. Verwende für die multivariate Regression als abhängige Variable den Preis und wähle dir mehr als eine unabhängige Variablen.

1. Setze ein Modell $y_i=f(x_i)=\beta x_i+\epsilon_i$ voraus, $y_i$ sind dabei die gefahrenen Kilometer und $x_i$ das Alter in Tagen. Bestimme $\beta$ so, dass $\sum_{i=1}^{n}(y_i-\beta x_i)^2=\text{RSS}(f)$ minimal ist, das heisst, leite eine Formel für $\beta$ her.
2. Berechne $\beta$ in Python ohne Hilfsmittel, das heisst, lies die Daten ein und bestimme $\beta$.
3. Verwende dann SciKit um ebenfalls $\beta$ zu bestimmen.
   1. Installiere zuerst scikit. Frage Ks oder eine/n der erfahrenen Programmierer/innen.
   2. Arbeite die Lösung unten Schritt für Schritt durch, falls du noch nicht klar kommst.
4. Leite die Formel für $\alpha$ und $\beta$ im Modell $f(y_i)=\alpha+\beta x_i$ her: Das Prinzip ist dasselbe: Wir haben neu eine Funktion $f$, welche von $\alpha$ und $\beta$ abhängt, das heisst, um $\alpha$ und $\beta$ zu bestimmen, kann $f$ nach $\alpha$ und nach $\beta$ abgeleitet werden, beide gleich Null gesetzt werden und das Gleichungssystem aufgelöst werden.
5. Berechne $\alpha$ und $\beta$ wiederum «von Hand» und dann in SciKit.
6. Du hast nun ein Modell: $y=f(x)=\alpha+\beta x$. Berechne Forecasts auf diesem Datensatz. Speichere deine Forecasts im Wiki Forecasts

import numpy as np
from sklearn.linear_model import LinearRegression
import matplotlib.pyplot as plt
 
#daten laden
path = "C:/pfad/zur/datei"
 
data =  np.loadtxt(fname = path, delimiter = ',')
#relevante spalten auswählen
x = data[:,8]
y = data[:,7]
 
#zähler und nenner definieren
num = 0.0
den = 0.0
for i in range(len(x)):
    num += y[i]*x[i]
    den +=  x[i]*x[i]
beta=num/den
print(beta)
 
#etwas weniger händisch
print(np.dot(x,y)/np.dot(x,x))
 
# mit scikit tools
#zuerst in einen echten mehrdimensionalen nx1-Array verwandenln
xb = x.reshape(-1,1)
 
 
#Ohne Achsenabschnitt
reg = LinearRegression(fit_intercept=False).fit(xb, y)
# alpha und beta ausgeben
print(reg.intercept_)
print(reg.coef_)
 
#Mit Achsenabschnitt
reg = LinearRegression(fit_intercept=True).fit(xb, y)
# alpha und beta ausgeben
print(reg.intercept_)
print(reg.coef_)
 
# Plot outputs
plt.scatter(xb, y,  color='black')
plt.plot(x, reg.predict(xb), color = "green")
 
plt.xticks(())
plt.yticks(())
 
plt.show()

Das Modell $y_i=\alpha+\beta x_i$ ist sehr simpel. Um gute Vorhersagen zu machen, müssen wir mehr als eine Variable haben, das heisst, wir hätten gerne ein Model $Y=\alpha+\beta_1X_1+\beta_2X_2+\cdots +\beta_pX_p$. Interpretiert man die Multiplikation $\cdot$ als Skalarprodukt, so kann dieses Modell einfach als $Y=\alpha +\beta\cdot X$ geschrieben werden. Dabei ist $\beta=[\beta_1,\ldots,\beta_p]$ und $X=[X_1,\ldots,X_p]$. Mit $\beta\cdot X=\langle \beta,X\rangle$ ist dann $Y=f(X)=\alpha +\beta\cdot X=\alpha+\beta_1X_1+\beta_2X_2+\cdots \beta_pX_p$. Genau gleich wie vorher suchen wir wieder $\alpha,\beta_1,\ldots,\beta_p$ so, dass $\text{RSS}(f)$ minimal ist, also \[ \sum_{i=1}^n (y_i-\alpha-\beta_1 x_i^1-\cdots-\beta_px_i^p)^2 \] soll minimal sein. Wenn also z.B. $p=2$ ist suchen wir also eine Ebene, welche die quadrierten Abstände der Datenpunkte von der Ebene minimiert.

| prA3.py

class Foo:
    def __init__(self,a):
        self.n = a
    def mehr(self):
        self.n+=1
    def show(self):
        print(self.n)
 
 
a=Foo(3)
b=Foo(5)
a.mehr()
b.show()
print(b.n)
b.mehr()
b.show()
print(b.n)
a.show()
print(a.n)
 
#a.n ist analog zu reg.coef_ oder reg.intercept_