KW35: Julia Mengen
Im Gegensatz zur Mandelbrotmenge (Einzahl) sprechen wir jetzt von Julia Mengen (Mehrzahl). D.h. es gibt nicht eine Julia Menge, sondern beliebig viele!? Wie ist das gemeint?
Bei der Mandelbrotmenge betrachteten wir die Zahlenfolge $$z_{n+1}=z_n^2 + c, \qquad \text{mit }z_0=0.$$ Dabei war $c$ ein beliebiger Punkt der Gauss'schen Zahlenebene, welcher die Eingangsgrösse der Zahlenfolge ist.
Bei der Julia Menge betrachten wir beliebige Funktionenfolgen, welche auf ganz $\mathbb{C}$ (oder auf ganz $\mathbb{C}$ mit einer endlichen Menge von Definitionslücken) definiert sind. D.h. $$z \mapsto f(z) \mapsto f(f(z)) \mapsto f(f(f(z))), \dots$$ Abhängig vom Startwert z kann diese Folge zwei grundlegend verschiedene Verhalten zeigen:
- Eine kleine Änderung des Startwertes führt zu praktisch der gleichen Folge, die Dynamik ist in gewissem Sinne stabil: Der Startwert wird der Fatou-Menge zugeordnet.
- Eine noch so kleine Änderung des Startwertes führt zu einem komplett anderen Verhalten der Folge, die Dynamik hängt „chaotisch“ vom Startwert ab: Der Startwert gehört zur Julia-Menge.
Siehe dazu Wikipedia-Julia-Mengen
Eine einfaches $f$ sind die quadratischen Funktionen $z^2+c$. Dies führt zur folgenden Funktionenfolge $$z_{n+1}=z_n^2+c$$ Mit $z_0$ als einen beliebigen Punkt aus der Gauss'schen Zahlenebene und $c\in\mathbb{C}$ als beliebigen, aber fixen Parameter. D.h. für jedes $c\in\mathbb{C}$ entsteht eine andere Julia Menge.
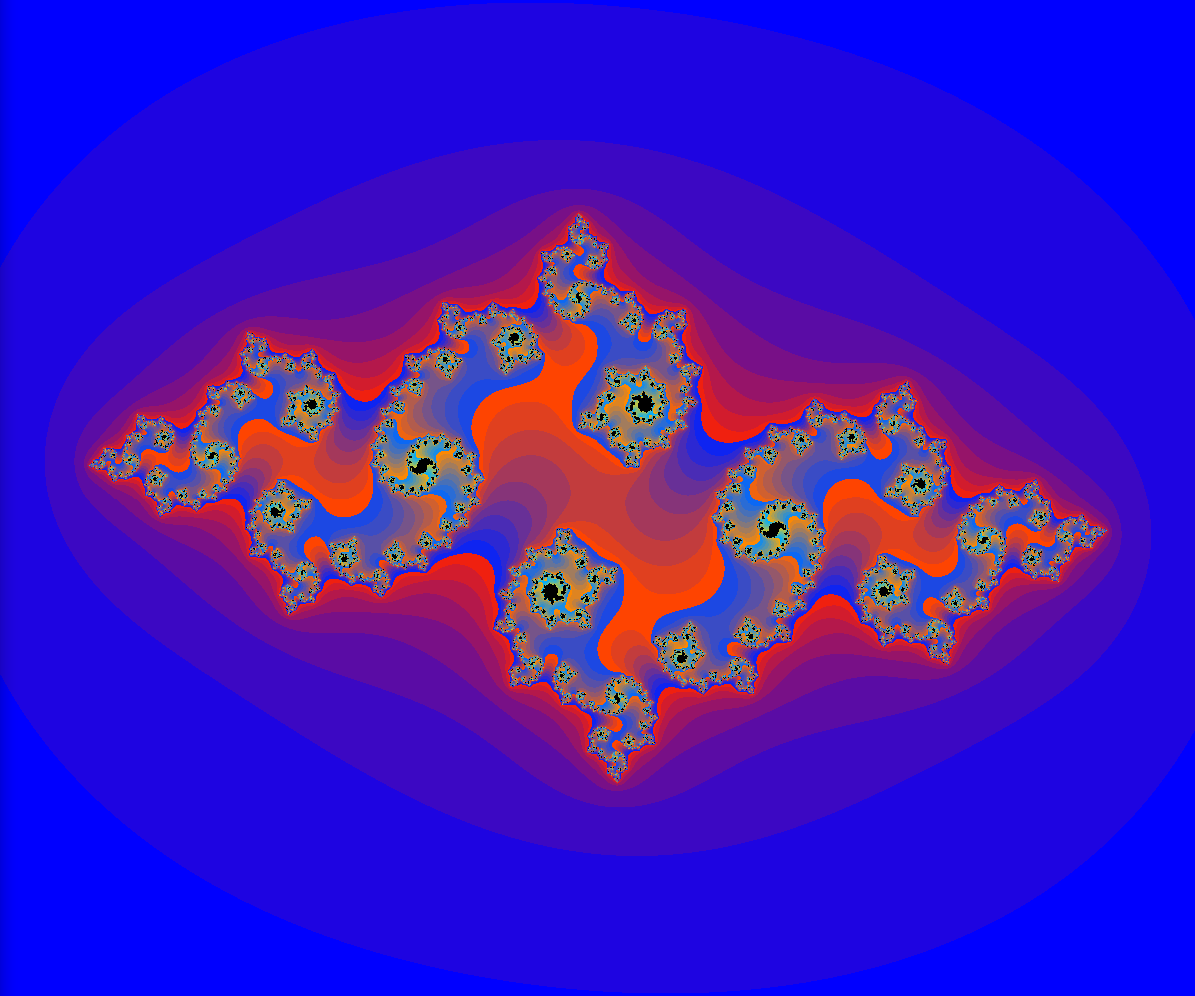
- Für $c=-0.6+i\cdot 0.6$ ergibt sich folgendes Bild.
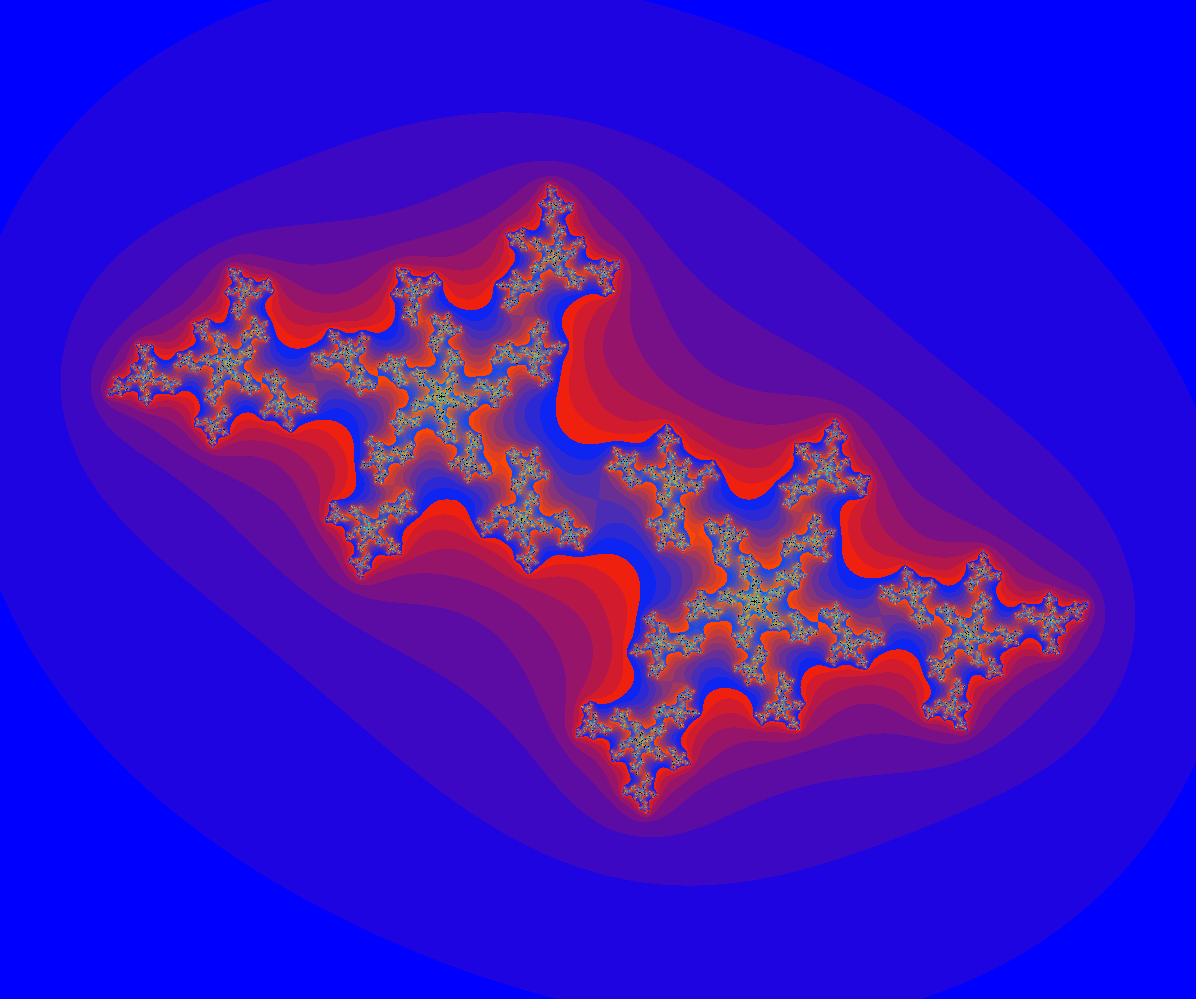
- Für $c=-0.8+i\cdot 0.2$ ergibt sich folgendes Bild.
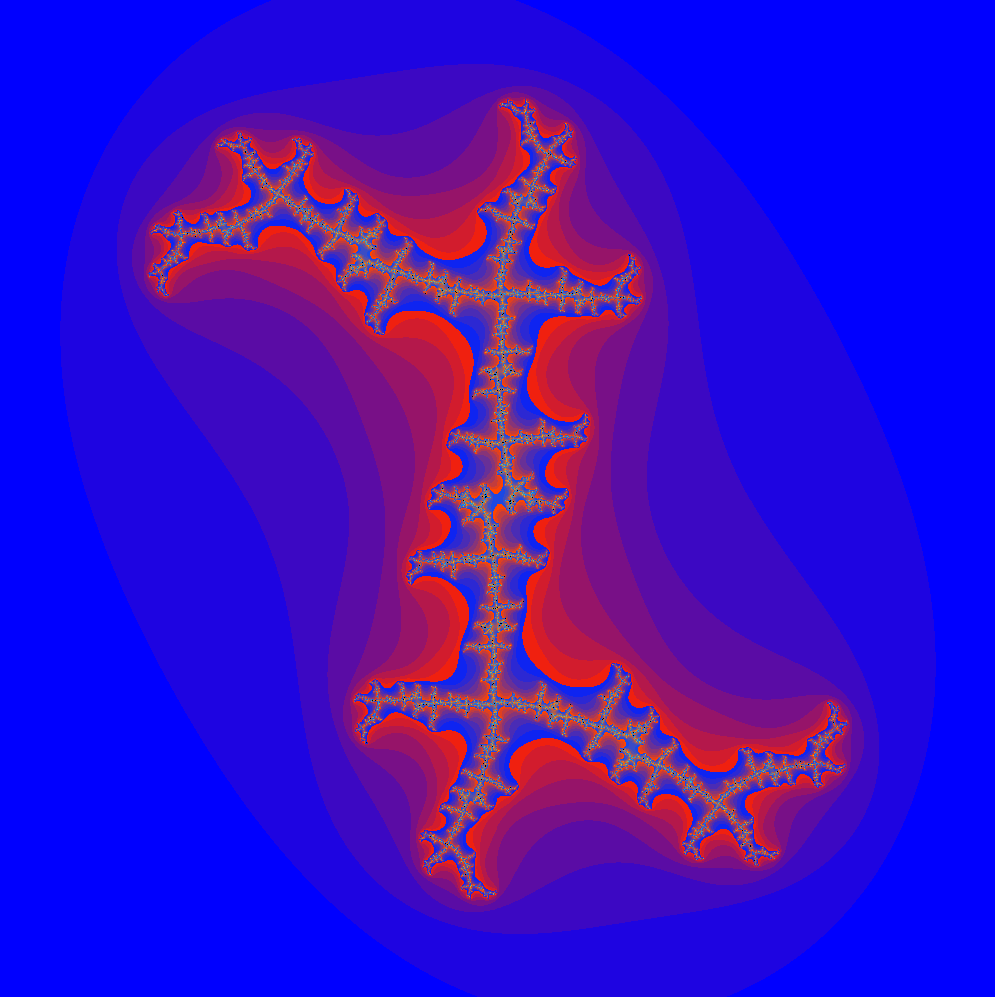
- Für $c=0.39+i\cdot 0.6$ ergibt sich folgendes Bild.
Aufgabe 1
- Passe dein Programm von letzter Woche (Mandelbrotmenge) so an, dass du Juliamengen darstellen kannst.
- Variiere den Parameter $c\in\mathbb{C}$ um verschiedene Juliamengen zu erzeugen.
- Verfeinere deine Farbgestaltung, siehe dazu Hard zoom.
Skalierung
Die Schrittweite in der Software soll nun so gewählt werden, dass sie genau dem Abstand von einem Pixel auf dem Bildschirm entspricht. D.h. jeder Punkt in der Software entspricht genau einem Punkt auf dem Bildschirm. Damit stellen wir sicher, dass wir
- genau die Anzahl von Punkten berechnen, die wir auch darstellen können.
- keine weissen Linien bekommen, weil die Pixel auf dem Bildschirm genau mit den Punkten in der Software übereinstimmen. Siehe dazu das nächste Bild als schlechtes Beispiel.
Mit
makeGPanel(Size(xPixel,yPixel))
wird ein GPanel mit der Grösse xPixel mal yPixel erzeugt. Im GPanel lässt sich mit dem Befehl
window(xmin, xmax, ymin, ymax)
ein Koordinatensystem hineinlegen. Damit kann die Schrittweite bestimmt werden. Es gilt: $$dx=\frac{x_{max}-x_{min}}{xPixel}\qquad\text{und}\qquad dy=\frac{y_{max}-y_{min}}{yPixel} $$Achtung: xPixel und yPixel sind ganze Zahlen. Arbeite deshalb bei der Berechnung mit einer Typenkonvertierung!
xPixel=int((xmax-xmin)/dx)
Aufgabe 2
- Ändere die Programme für die Julia Mengen und die Mandelbrotmenge so ab, dass die Schrittweite genau einem Pixel entspricht.
Aufgabe 3
- Ändere in der Rekursionsvorschrift den Exponenten und wiederhole die Aufgabe 1.
- Ändere die Rekursionsvorschrift auf eine beliebige interessante auf $\mathbb{C}$ definierte Funktion ab und wiederhole die Aufgabe 1.
Kurven
Aus dem GF Mathematik kennen wir die Kreisgleichung. $$K=\{(x|y)\in\mathbb{R}^2 | (x-x_0)^2+(y-y_0)^2=r^2\} $$ Dabei gilt:
- $r$ ist der Kreisradius
- $M$ ist das Kreiszentrum mit den Koordinaten $x_0$ und $y_0$
Um Graph des Kreieses lässt sich nicht als Funktion darstellen. Etwas unschön, aber machbar wäre der obere Halbkreis und der untere Halbkreis jeweils als Funktion aufzuschreiben. $$K_{oh}:\quad y=y_0+\sqrt{r^2-(x-x_0)^2} \quad\text{mit} \quad x_0-r\leq x \leq x_0+r $$ und $$K_{uh}:\quad y=y_0-\sqrt{r^2-(x-x_0)^2} \quad\text{mit} \quad x_0-r\leq x \leq x_0+r $$
Parametrisierte Kurven
Eine parametrisierte Kurve $c$ ist eine Abbildung eines Intervalls in den n-dimensionalen Raum. Betrachten wir die Ebene, dann ist $n=2$, betrachten wird den Raum, dann ist $n=3$. $$c:\mathbb{R}\supset I \rightarrow \mathbb{R}^2, t \mapsto \left( \begin{array}{c} x(t)\\y(t) \end{array} \right)$$ Eine mögliche Parametrisierung eines Kreises in der Ebene ist $$K: \left[0,2\pi\right] \rightarrow \mathbb{R}^2, t \mapsto \left( \begin{array}{c} x_0 + r\cdot \cos(t)\\y_0 + r\cdot \sin(t) \end{array}\right)$$ Eine andere Parametrisierung ist $$K: \left[0,1\right] \rightarrow \mathbb{R}^2, t \mapsto \left( \begin{array}{c} x_0 + r\cdot \cos(2\pi \cdot t)\\y_0 + r\cdot \sin(2\pi \cdot t) \end{array}\right)$$ Aufgabe 4
- Schreibe eine Funktion, die einen Kreis zeichnet. Als Parameter werden der Radius $r$ und das Kreiszentrum $Z=(x_0,y_0)$ übergeben.
Kardioide
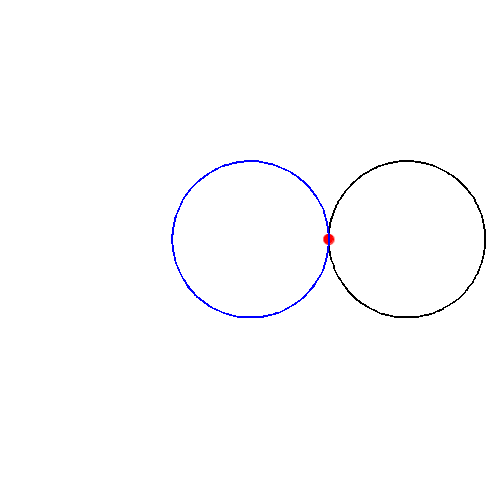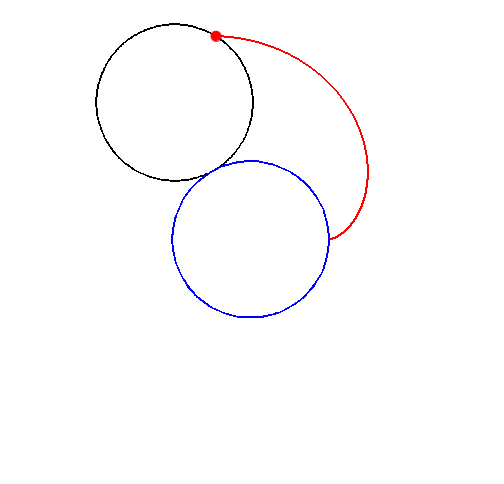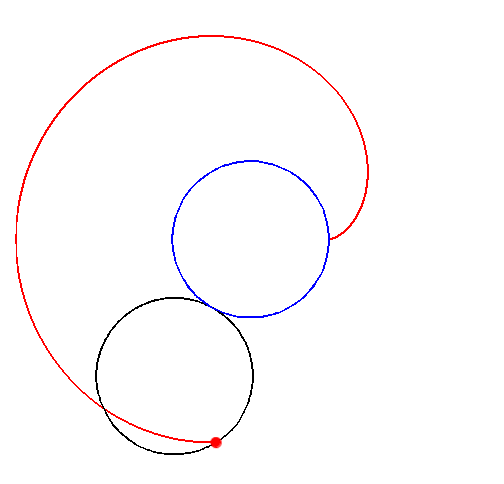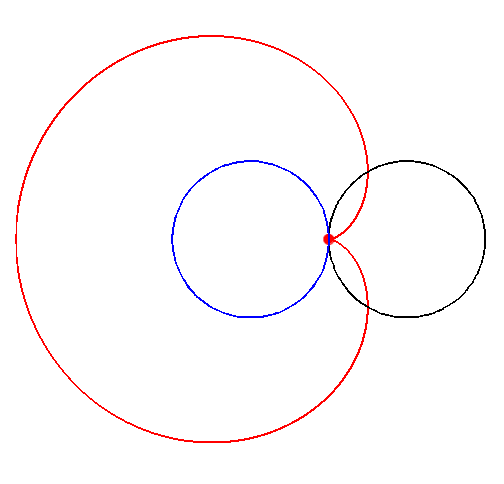
Betrachten wir einen Punkt $P$ auf einem Kreis $K_1$ mit Radius $r$, welcher sich auf einem zweiten Kreis $K_2$ mit dem gleichen Radius $r$ abrollt. Dabei entsteht die Herzkurve, auch Kardioide genannt.
Diese Bild sollte euch bekannt vorkommen. Wo habt ihr die Kardioide im EF CG schon gesehen?
Aufgabe 5
- Wir bestimmen eine Parametrisierung der Kardioide. Dabei betrachten wir zuerst den allgemeinen Fall, d.h. Sei $r$ der Radius des Kreises $K_1$ und sei $R$ der Radius des Kreises $K_2$.