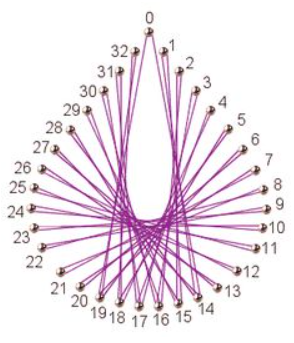
n-Tables
Aus unserer Kindheit kennen wir Fadenbilder. Etwas ähnliches wollen wir diese Woche programmieren.
Dazu ordnen wir $k$ Punkte in einem Kreis mit Radius $R=100$ symmetrisch an. Die Punkte werden dabei durchnummeriert, beginnend bei 0. Bei einen n-Table wird der Punkt mit der Nummer $i$ mit dem Punkt $n\cdot i$ verbunden.
Für ein $n=2$ ergeben sich folgende Verbindungen:
- 0 zu 0 (keine Linie)
- 1 zu 2
- 2 zu 4
- 3 zu 6
- 4 zu 8
- …
- k-2 zu (2k-4) mod k
- k-1 zu (2k-2) mod k
Aufgabe 1
- Erstelle ein 2-Table mit k=30 Punkten
Dazu einige Tipps:
Die Punkte liegen alle auf einem Kreis mit Radius 100 um den Koordinatenursprung. Die Koordinaten sind dann $$x(\varphi)=R\cdot \cos(\varphi) \qquad \text{und} \qquad y(\varphi)=R \cdot \sin(\varphi) $$ Der Winkel $\varphi$ hängt von der Punktnummer ab. Für die Winkeländerung von Punkt zu Punkt gilt: $$\Delta \varphi = \dfrac{2\pi}{k}$$ Damit gilt $$x(i)=R\cdot \cos(\Delta\varphi\cdot i) \qquad \text{und} \qquad y(i)=R \cdot \sin(\Delta\varphi\cdot i) $$Sinnvollerweise werden die Punkte einmal berechnet und in einer Liste Punkte abgelegt. Nachher muss nur die Liste durchlaufen werden und der Punkt n wird mit dem Punkt 2n mod k verbunden. Dazu verwenden wir den Befehl line(xStart,yStart,xEnd,yEnd).
Aufgabe 2
- Um das Bild zu verfeinern setze k=200 Punkte
- Erweitere eine Programm so, dass k von 30 bis 200 schrittweise durchläuft. Warte nach jedem Bild 100 ms.
- Welches Bild ergibt sich?
Aufgabe 3
- Ändere dein Programm so ab, dass n-Tables von n=2 bis n=100 für ein k=200 erstellt werden. Warte nach jedem Bilde 200ms.
- Ändere dein Programm so ab, dass du über ein Eingabefenster dein $n$ eingeben kannst. Mit einer Eingabe von n<2 beendest du dein Programm.
- Ändere dein Programm so ab, dass du mit den Pfeiltasten Up und Down das $n$ vergrössern und verkleinern kannst. Schreibe jeweils die Nummer eines $n$-Table über das Bild.
Aufgabe 4
Je ein Profi und ein Bachelor / eine Bachelorette setzen sich zusammen und analysieren die Aufgabe 3.3. Als Guideline kann das obige Programm dienen. Der Profi ist Coach und hilft bei Unklarheiten.
Ziel der Aufgabe
Alle Teilnehmer vom EF CG verstehen, wie ein parametrisiertes n-Table realisiert wird und wie die Parameterübergabe bei einer Tastatureingabe funktioniert.