Trigonometrie
mit Eintragungen während der Lektionen:
Beachte unten insbesondere den Abschnitt zu harmonischen Schwingungen.
Ergänzungen (etwa Animationen zu Sinus und Cosinus)
Velo-Rad als Motivation für Sinus- und Cosinus (Speed 0.5, Start at 0:06): https://www.youtube.com/watch?v=lFRncepeqC4
Nach Aufgabe 12.3 zeigen:
Bei Aufgabe 12.5 könnte das Folgende ergänzen (ist aber bereits Repetitionsaufgabe): $\cos(\alpha + 90^\circ) = -\sin(a)$ und $\sin(\alpha + 90^\circ) = \cos(a)$. Dies erklärt nämlich (zusammen mit anderer Formel aus der Aufgabe), dass der Taschenrechner korrekterweise $\cos(55^\circ) = \sin(35^\circ)$ liefert. Eventuell allgemein zeigen lassen: $\cos(45^\circ + \alpha)=\sin(45^\circ-\alpha)$: Entweder als Folgerung aus den obigen Sachen oder direkt per Spiegelung an der ersten Winkelhalbierenden.
Zu Aufgabe 12.6: Für die meisten Winkel kann man $\cos(\alpha)$ und $\sin(\alpha)$ nur näherungsweise berechnen. Für die in dieser Aufgabe angegebenen Winkel kann man diese Werte aber rein auf Grund geometrischer Überlegungen (ohne Taschenrechner bzw. Ablesen) exakt bestimmen. Für weitere Winkel, wo dies exakt möglich ist, siehe etwa https://en.wikipedia.org/wiki/Sine_and_cosine#Special_values.
Zum Messen von Winkeln: Dass wir den Vollwinkel mit $360^\circ$ bezeichnen (und nicht mit irgendeiner anderen Zahl), ist historisch bedingt. Es gibt mehrere Theorien, warum das so ist:
- Die Sonne verschiebt sich von der Erde aus gesehen jeden Tag um einen Winkel von etwa einem Grad vor dem Fixsternhimmel. Dies hängt damit zusammen, dass das Jahr etwa 360 Tage hat, was man landwirtschaftlich/biologisch bzw. astronomisch beobachten kann: Wann “startet” der Frühling, also die Wachstumsperiode in der Natur? Wie lange dauert es, bis derselbe Fixsternhimmel wieder sichtbar wird (um Mitternacht)?
- Der Winkel im gleichseitigen Dreieck (ein Sechstel des Vollwinkels) ist besonders “schön”. Da die Bablylonier im Sexagesimalsystem rechneten (also mit Basis 60 statt der Basis 10 im Dezimalsystem), teilten sie diesen Winkel in 60 gleich grosse “Einheitswinkel” von einem Grad.
- Die Zahl 360 hat besonders viele Teiler (nämlich 1, 2, 3, 4, 5, 6, 8, 9, 10, 12, 15, 18, 20, 24, 30, 36, 40, 45, 60, 72, 120, 180, 360). Dies hat zur Folge, dass man im $360^\circ$-System sehr viele Winkel durch natürliche Zahlen angeben kann: Teilt man beispielsweise den Vollwinkel in 15 gleiche Teile, so erhält man einen Winkel von $\frac{360^\circ}{15} = 24^\circ$.
Graphen der Arcus-Funktionen mit Geogebra verstehen
- Arcus-Sinus: https://www.geogebra.org/classic/xecstfrx
- Arcus-Cosinus: https://www.geogebra.org/classic/sjpg2vrq
- Arcus-Tangens: https://www.geogebra.org/classic/g3nvsp3g
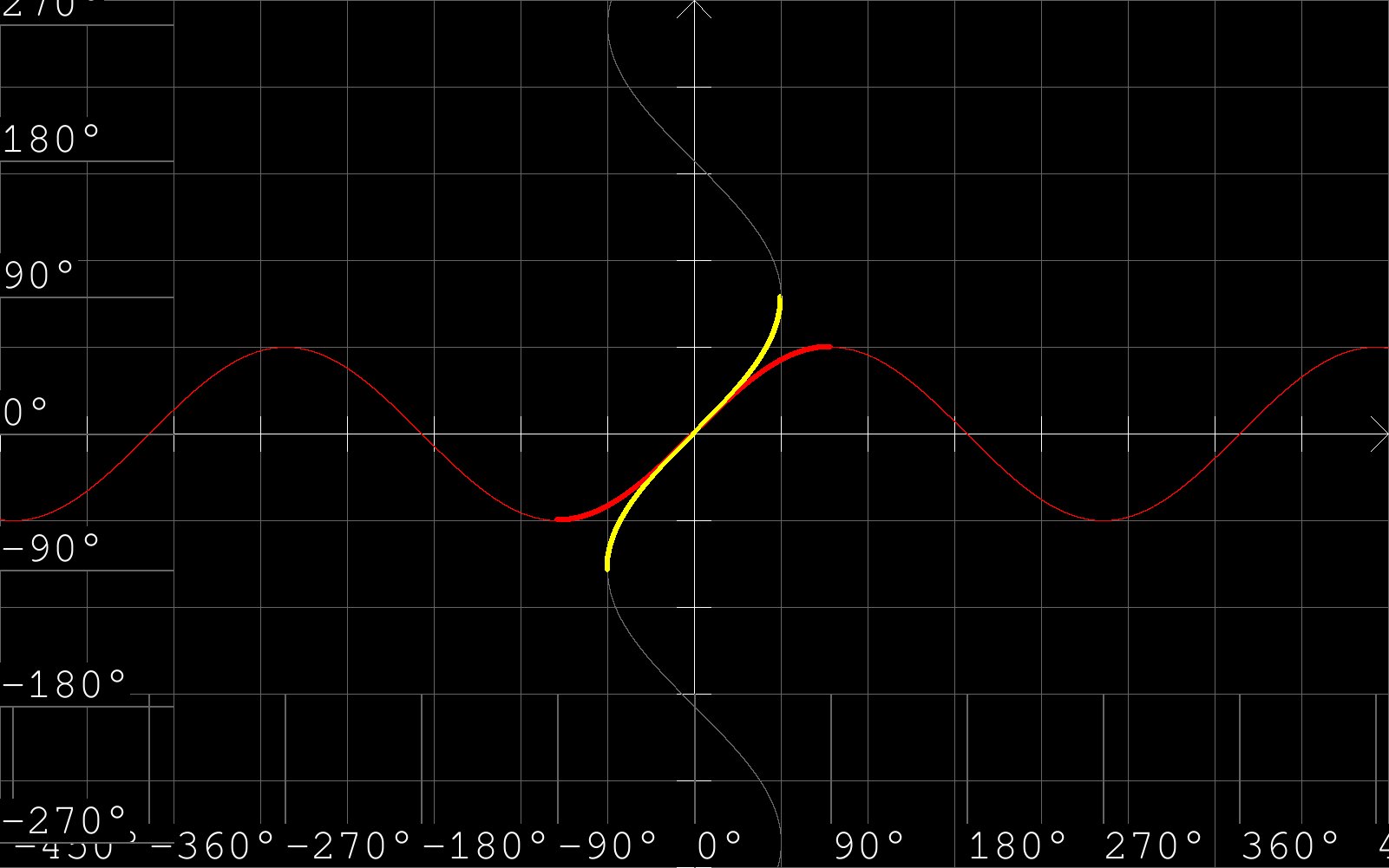
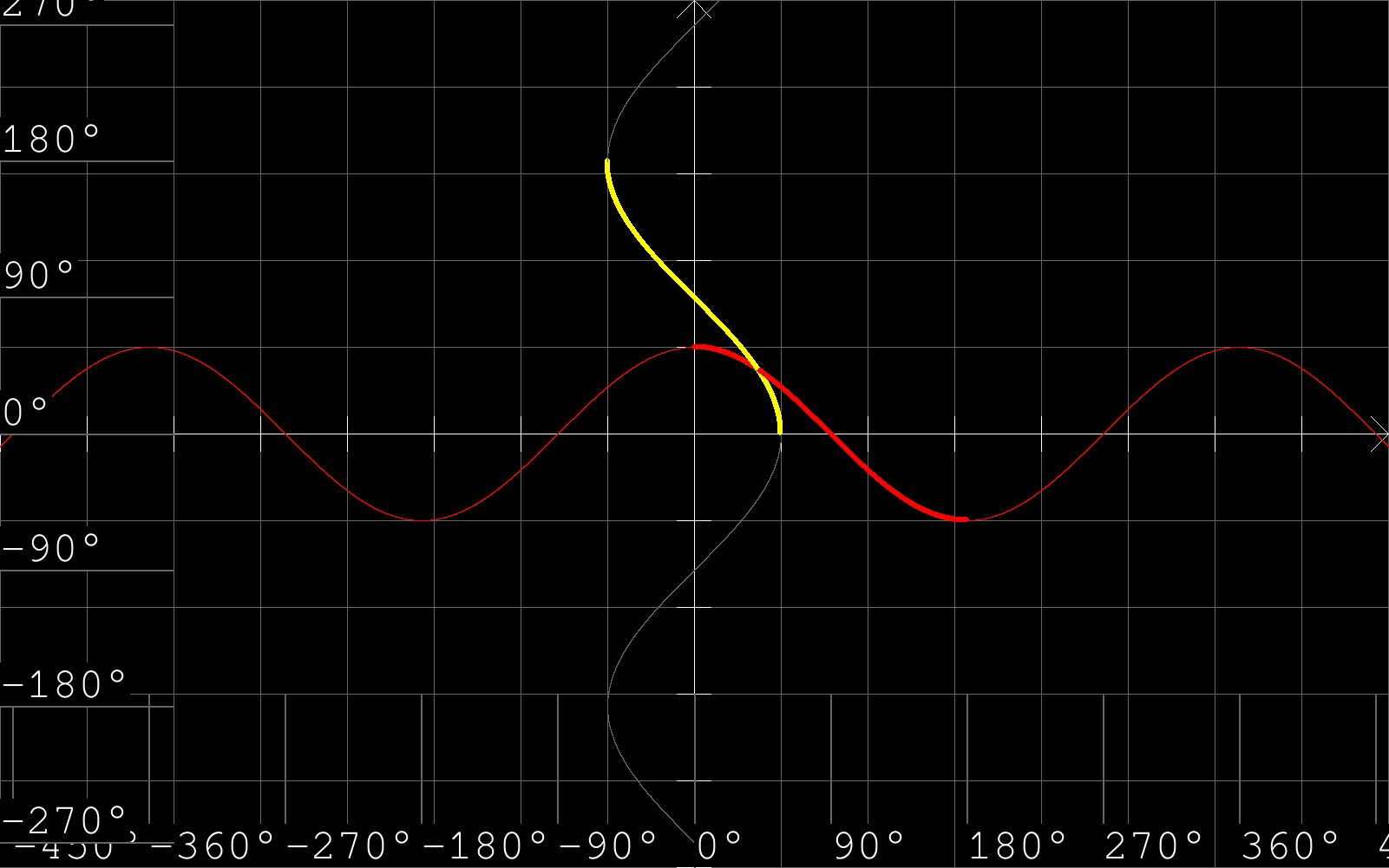
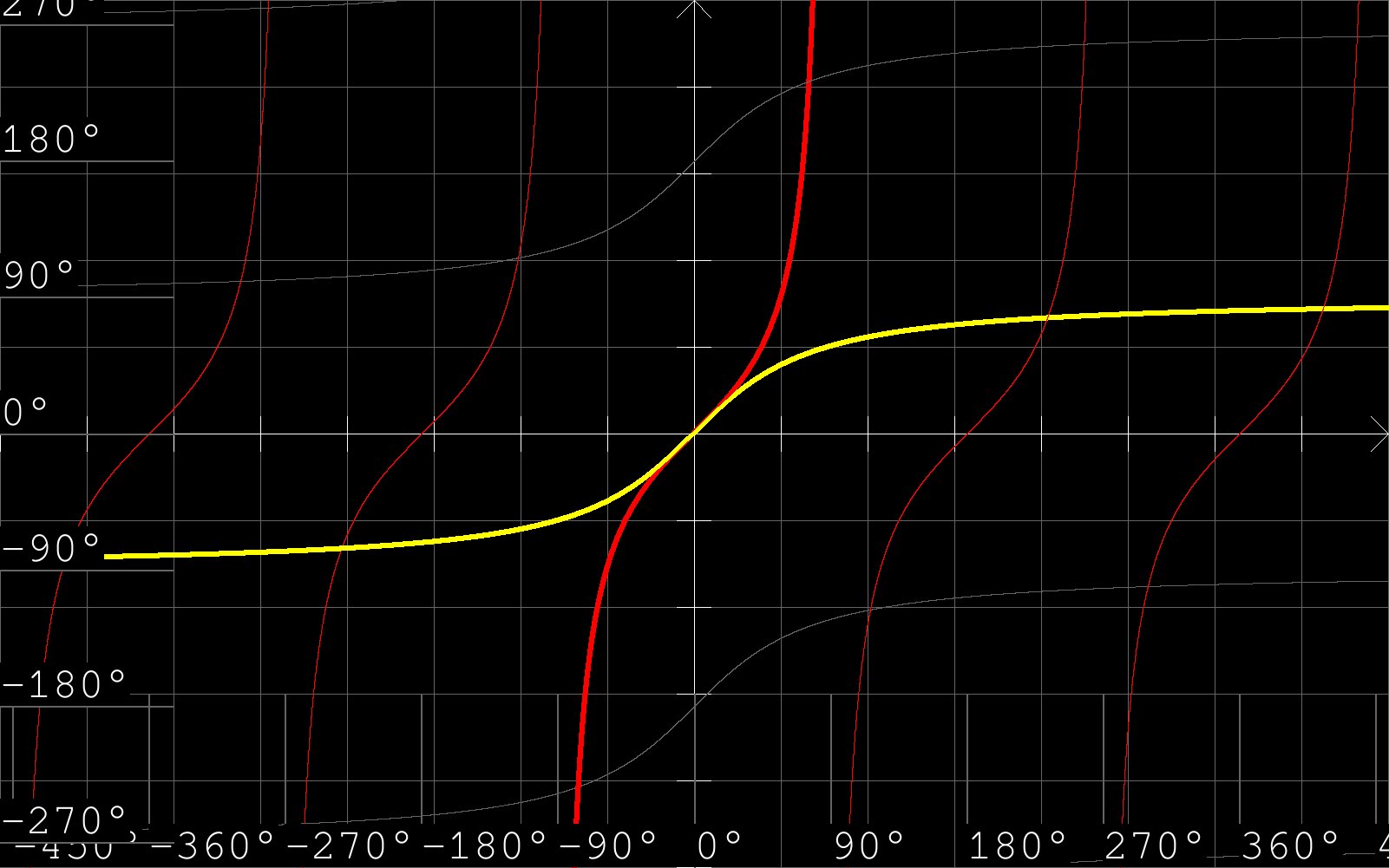
Beachte, dass für jede trigonometrische Funktion der Graph der zugehörigen Arcus-Funktion aus dem Graphen der betrachteten trigonometrischen Funktion (bzw. genauer aus einem gewissen Teil davon) durch Spiegelung an der ersten Winkelhalbierenden hervorgeht (was dem Vertauschen von $x$- und $y$-Koordinate aller Punkte entspricht). Der Grund ist folgender: Jede trigonometrische Funktion ordnet einem Winkel eine Zahl zu (die Koordinaten eines (vom Winkel abhängigen) Punktes bzw. die Steigung einer (vom Winkel abhängigen) Geraden). Die zugehörige Arcus-Funktion ordnet umgekeht einer Zahl einen Winkel zu.
Graphen von arcsin bzw. arccos bzw. arctan als dicke gelbe Linie
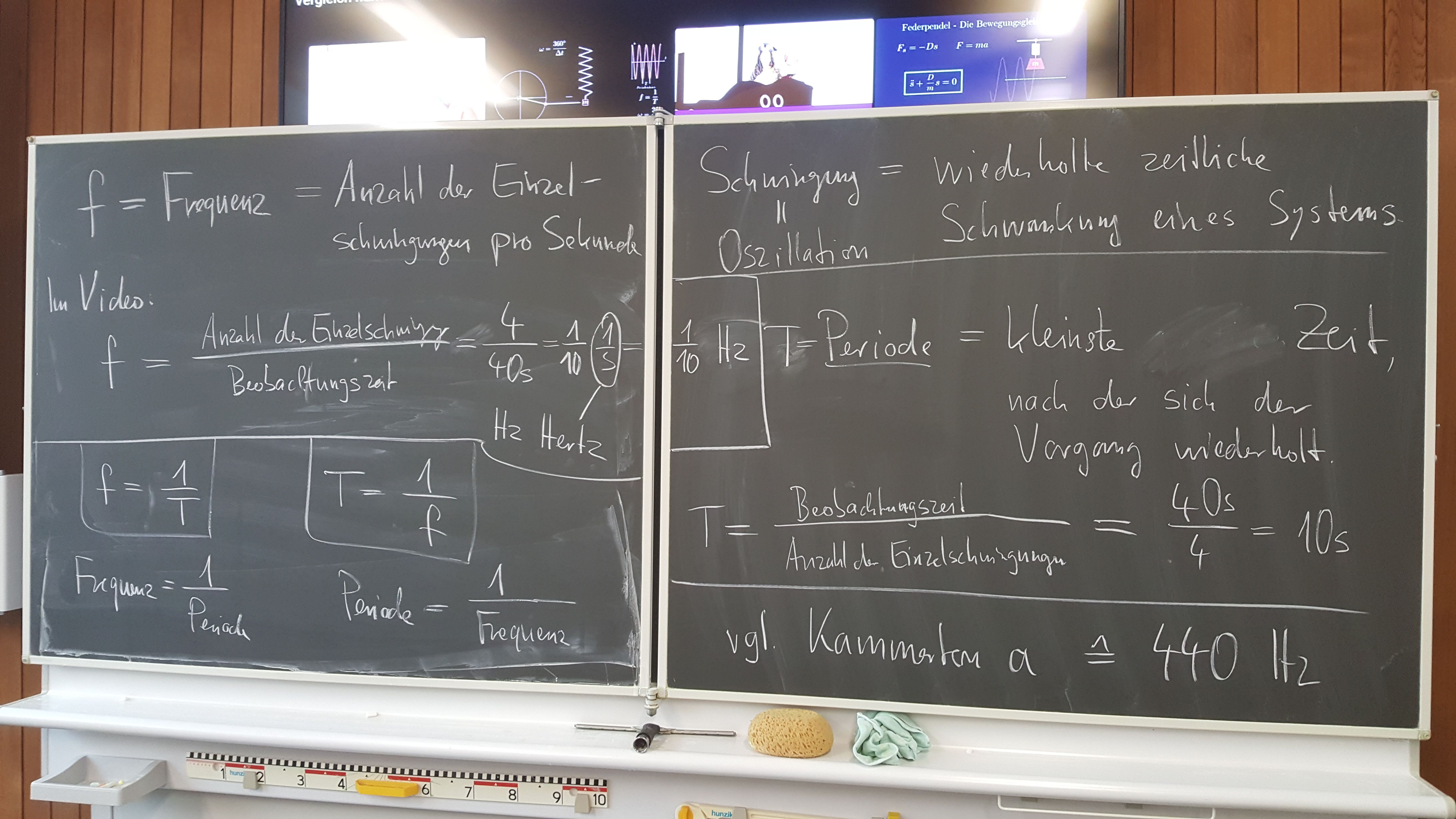
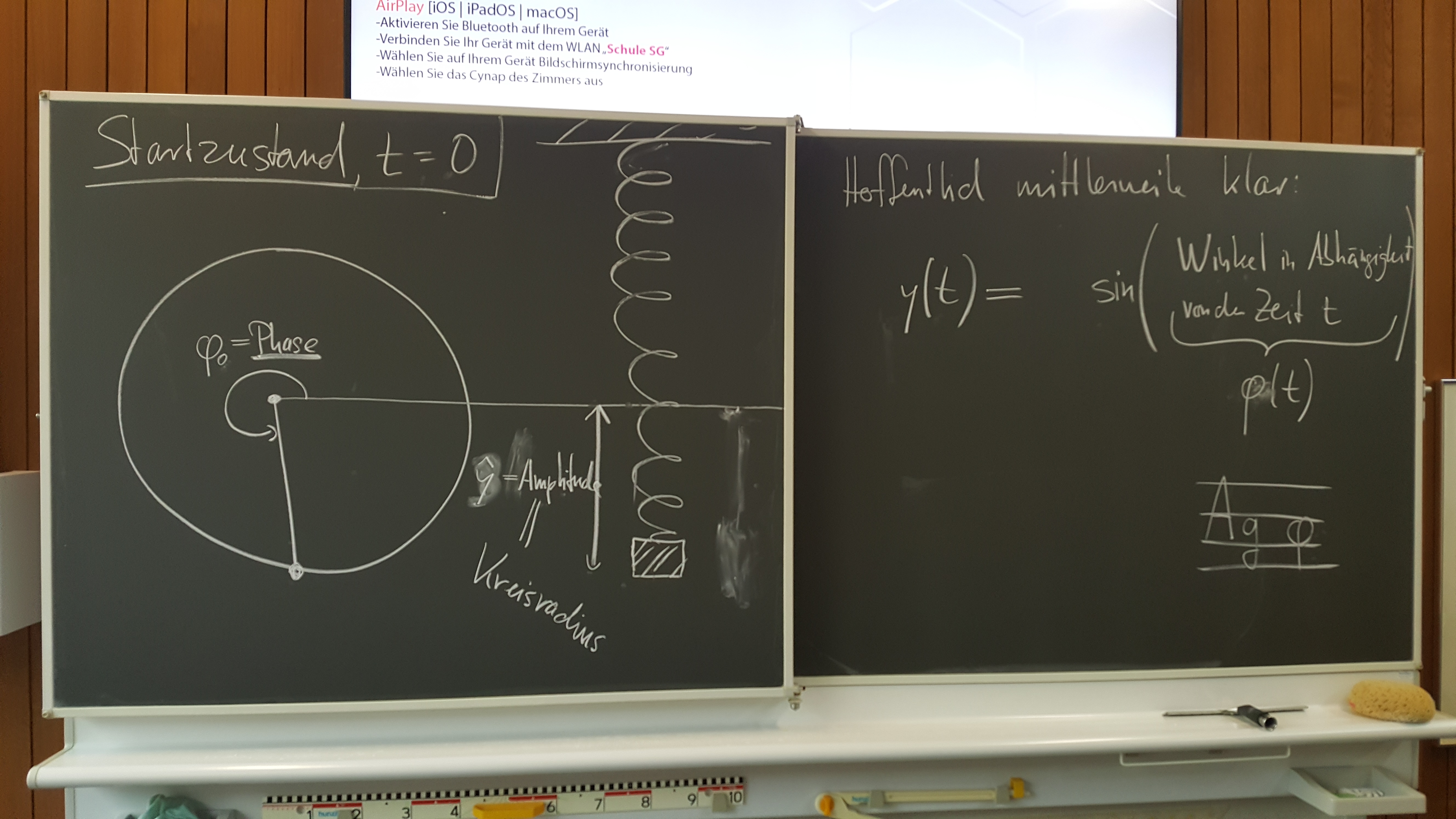
Einführung in harmonische Schwingungen
Meine Vorbereitung: einfuehrung-harmonische-schwingungen.pdf
In Lektion verwendet:
- Federpendel vs. Kreisbewegung: https://www.youtube.com/watch?v=ZZiE8KbkTuw
- evtl. 1:51 und 4:36 in https://www.youtube.com/watch?v=GqkND_7Kcc8
Geogebra: Harmonische Schwingung zum Ausprobieren verschiedener Parameter: https://www.geogebra.org/classic/u89nmhhm
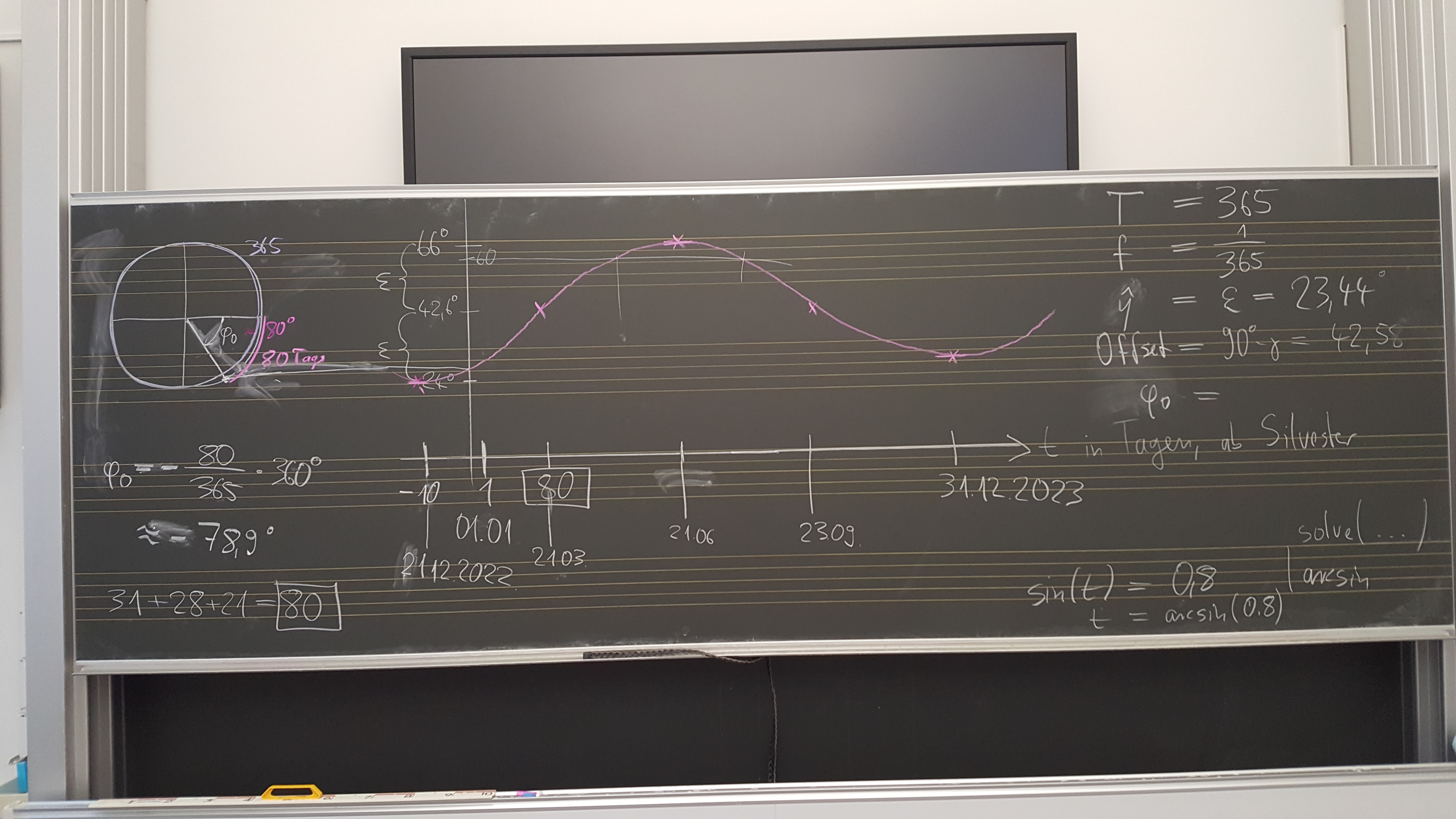
Astronomisches: Zu Aufgabe 12.17 (c) + (d)
Zur Lage der Ekliptik: viertes Bild auf https://www.rainerstumpe.de/Astro/sonnenbahn.html
- (d) blaue Linie (daylight) in erster Graphik
- (c) dritte Graphik (maximal sun altitude)
Wer will, kann (so wie ich für St. Gallen) auch selbst die geographischen Koordinaten seines Wohnorts ermitteln (per Karte oder Internet) und hier eingeben: https://ptaff.ca/soleil/