Table of Contents
Freifach Statistik
Links
Lektion 01
Ziele
Ziele der Lektion:
- Einführung Freifach
- Unterlagen erstellen: Eigenes Dossier anlegen
- Geräte und Tools kennenlernen
- Erste Berechnungen anstellen
Auftrag
- Einführungsvideo schauen.
- Mittlerer Verkaufspreis (Durchschnitt) aller Autos berechnen
- Mittlerer Verkaufspreis aller weissen Autos berechnen
- Anzahl grüne Autos berechnen
- Welches Modell ist am teuersten?
- Welche Farbe oder Energieeffizienz ist am günstigsten? Ist das für alle Modelle und Farben oder Energieeffizienz identisch?
Lektion 02/03a
Ziele der Lektion
- Unterlagen durcharbeiten.
- Der Begriff des Zufalls ist intuitiv bekannt bei Experimenten (Würfeln) wie auch erhobenen Daten (Autopreise): In Alltagssprache Zufall beschreiben.
- Jede/r kann ein Histogramm erstellen und interpretieren.
- Jede/r kann mit Excel Zufallszahlen erzeugen.
Aufträge:
- Eile-mit-Weile Auftrag ausführen
- Zuerst manuell mit Strichliste und Würfeln
- Nachher mit Excel simulieren. Hilfreiche Funktionen sind
WENN(),ZUFALLSZAHL(),RUNDEN()resp.AUFRUNDEN(),SUMMEWENN()etc. Eine mögliche Lösung ist hier zu finden. - Nachher mit R Simulieren. Hiflreiche Fuktionen sind entweder
sampleoderrunif,ceiling. Histogramme gibt's mithist
- Histogramm mit Excel oder Geogebra erstellen:
- Excel: Daten markieren, Einfügen → Alle Diagrammtypen → Histogramm
- Geogebra: Ansicht → Tabelle → Daten einfügen mit CTRL+V einfügen → Analyse einer Variable
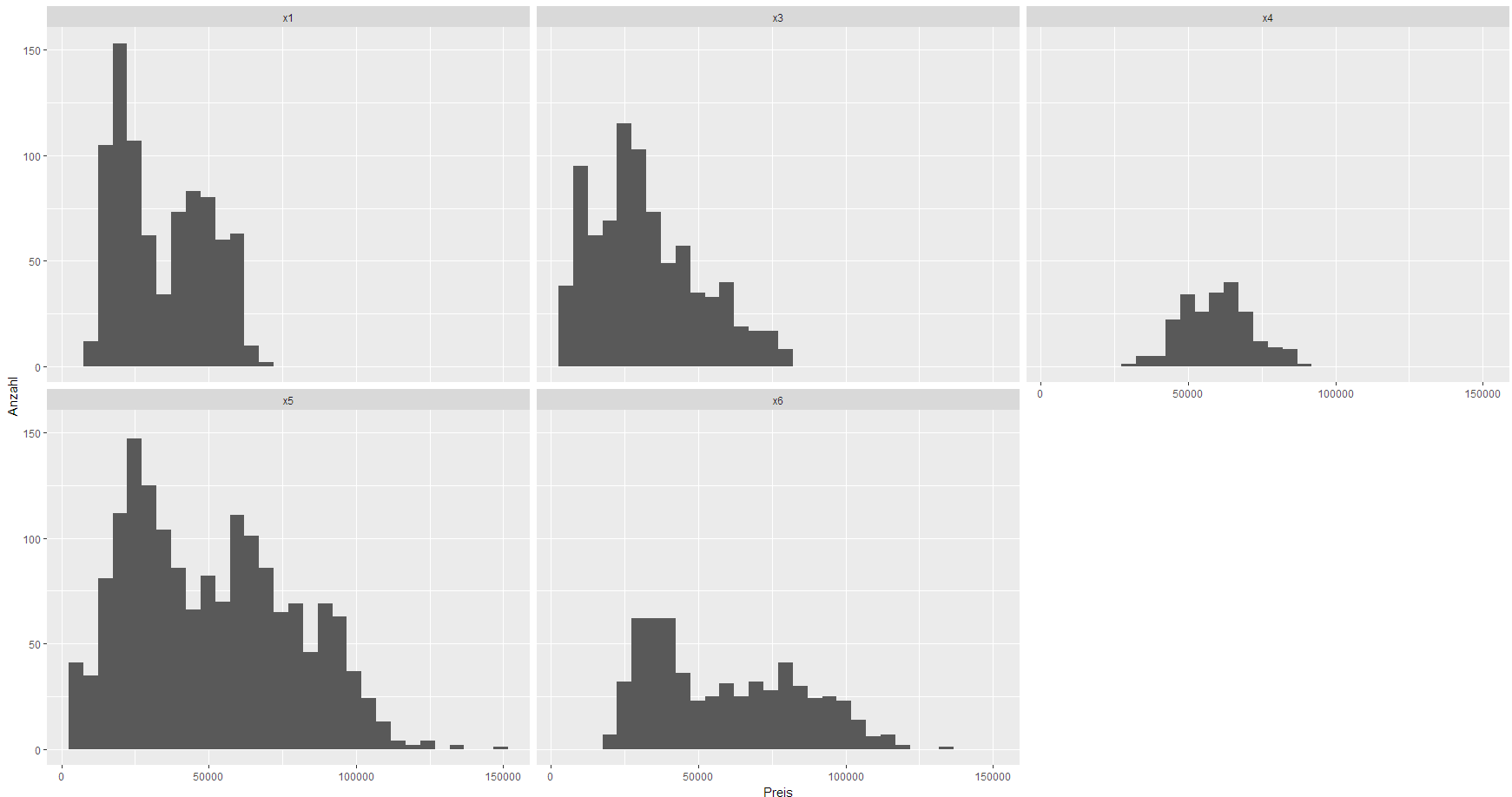
- Histogramm der Fahrzeugpreise (z.B. alle X1) erstellen
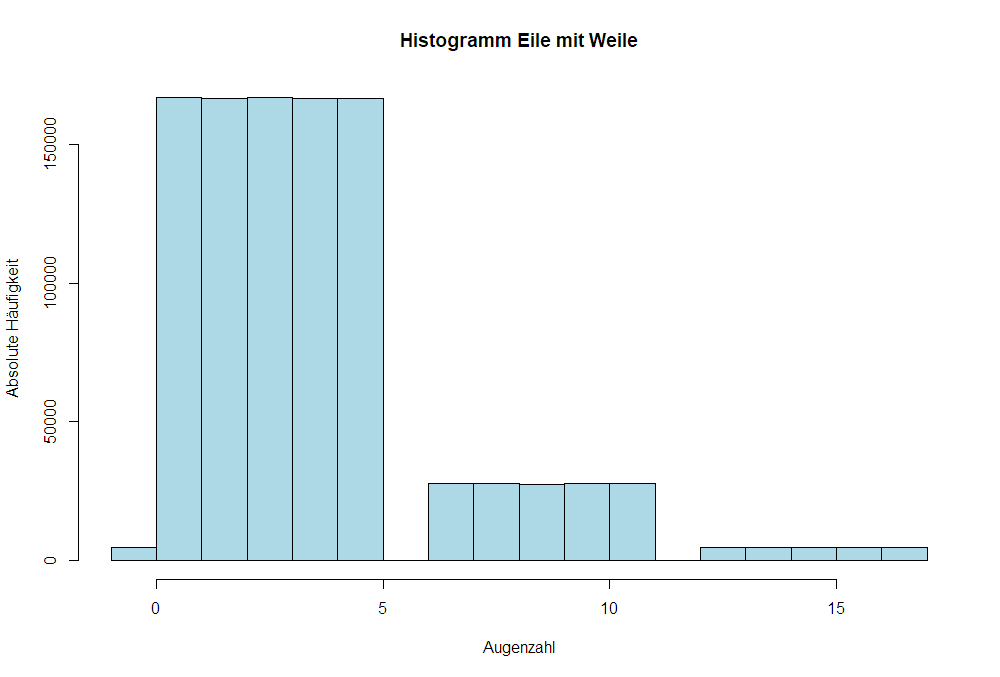
Histogramm Eile mit Weile bei 1'000'000 Würfeln
R Code Simulation Eile-mit-Weile
- eilemitweile.R
rollDie <- function() { isSix <- TRUE sum <- 0 while (isSix) { thissample <- sample(6, 1) if (thissample + sum > 18) break sum <- sum + thissample isSix <- thissample == 6 } if (sum == 18) { sum <- 0 } return(sum) } dier <- dier <- replicate(1e+06, rollDie()) hist(dier, breaks = seq(-1, 17), main = "Histogramm Eile mit Weile", xlab = "Augenzahl", ylab = "Absolute Häufigkeit", col = "lightblue")
Lektion 04
Ziele
- Jede/r kann ein Histogramm erklären.
- Jede/r kann Mittelwert, Modus, Median und beliebige Quantile von Hand und mit Excel/R ausrechnen (Lagemasse)
- Jede/r kann Varianz, Standardabweichung, IQA ausrechnen von Hand und mit Excel/R (Skalenmasse)
- Jede/r kann auf Grund einem Histogramm passende Lagen- und Skalenmasse zuordnen
Auftrag
- Definitionen auf Unterlagen vom letzten Mal nachlesen und mit Begriffen unten ergänzen.
- Berechne die genannten Grössen für
-2.9, 25.4, -12.3, -38.5, 4.2, 23.7, -0.4, 1.5, -23.3, 21.von Hand und mit Excel - Berechne für verschieden BMW Modelle ein Histogram und notiere Mittelwert, Median, Standardabweichung und IQA darunter. Mögliche Vorgehensweise dabei wäre
- Alle Preise in ein neues Tabellenblatt kopieren
- Jeweils in den ersten Zeilen die Grössen für die darunterliegenden Werte ausrechnen und dann Formeln nach rechts ziehen.
<h Lösung>
- Mittelwert: -0.15
- Modus: Nicht eindeutig.
- Standardbweichung: 20.70
- Varianz: 428.53
- Median: -0.45
- IQA: 26.825
</hidden>
Definitionen
Quantil
Ein Quantil gibt den dem Prozentrang zugehörigen Wert der Verteilung wieder. Der Median ist z.B. das 50% Quantil. Das 25%-Quantil z.B. ist der Wert, für welchen gilt, dass 25% der Werte kleiner und 75% der Werte grösser sind. Mathematisch kann man das wie folgt festhalten:
Möchte man das Quantil $\alpha=35\%=0.35$ von den $n=15$ Daten 10.6, 16.9, -27.3, 9.6, 18.1, -6.4, 34.4, 42.7, -3.6, 5, -3.2,
11.1, 46.1, 19.4, 2.4 berechnen, dso muss man diese zuerst sortieren: -27.3, -6.4, -3.6, -3.2, 2.4, 5, 9.6, 10.6, 11.1, 16.9, 18.1,
19.4, 34.4, 42.7, 46.1. Die sortierten Werte werden mit $x_{(1)},x_{(2)},\ldots,x_{(n)}$ bezeichnet. Man sucht dann diesen Wert so, dass der gefundene Wert dem geforderten Prozentrang von $\alpha=0.35$ am nächsten kommt.
Genauer: Sei $K=\lfloor\alpha\cdot n\rfloor+1$ wobei $\lfloor\cdot\rfloor$ auf die nächste ganze Zahl abrundet. Für uns ist also $K=\lfloor0.35\cdot 15\rfloor+1=\lfloor5.25\rfloor+1=5+1=6$. Wir nehmen also den 6. Wert: Damit ist $Q_{0.35}=x_{(6)}=5$
Ist aber $\alpha\cdot n$ eine natürliche Zahl so, so nehmen wir wegen des Abrundens den mittleren der beiden Werte $x_{(K-1)}$ und $x_{(K)}$: Für $\alpha=0.2$ ist $K=3+1=4$ und damit $Q_{0.2}=\frac12((-3.6)+(-3.2))=-3.4$. $$Q_\alpha=\begin{cases}x_{(K)}\text{ wenn $\alpha\cdot n$ nicht ganzzahlig}\\\frac12\left(x_{(K)}+x_{(K-1)}\right)\text{ wenn $\alpha\cdot n$ ganzzahlig}\end{cases}$$
Quartile
Quartile sind die $25\%$, $50\%$ und $75\%$ Quantile einer Verteilung. Für das erste Quartil gilt also, dass $25\%$ der Beobachtungen kleiner sind, $75\%$ der Beochbachtungen sind grösser.
Bei der Berechung der Quantile kommen bei unterschieldichen Softwarelösungen unterschiedliche Methoden zum Einsatz. Das heisst, u.U. stimmen die Quantile zweier unterschiedlichen Softwarelösungen nicht überein.
Interquartilsabstand (IQA)
Der Interquartilsabstand ist ein Mass für die Skala einer Verteilung. Wie weit sind das erste und dritte Quartil auseinander: $\text{IQA}=Q_{0.75}-Q_{0.25}$.
Lektion 05
Ziele
- Boxplot erstellen und interpretieren
- Lage und Skalenmasse auf Grund Boxplot und Kennzahlen interpretieren
Aufträge
- Boxplot
- Theorie Boxplot unten lesen
- Einen Boxplot von Hand der Daten 9, 6, 7, 7, 3, 9, 10, 1, 8, 7, 9, 9, 8, 10, 5, 10, 10, 9, 10, 8 erstellen.
- Einen Boxplot von Hand (mit Hilfe Excel) der Preise von einem BMW Modell (X1 bis X5) erstellen. Dabei soll sein: 1cm ≙ Fr. 10'000
- Einen Boxplot mit Geogebra (mit Excel geht es; ist aber aufwändig) erstellen.
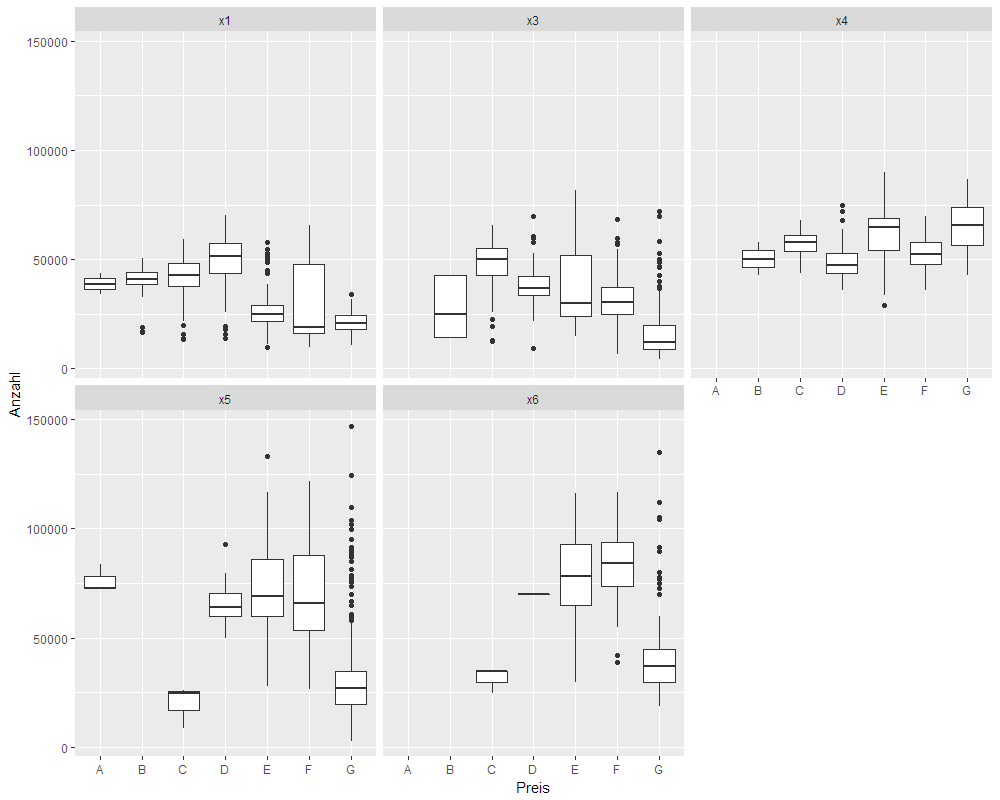
- Die BMW Boxplots den BMW Histogrammen zuordnen
- Die BMW Mittelwerte, Standardabweichungen, IQA, Median und $Q_{30\%}$ den Histogrammen und Boxplots zuordnen
- Ein Beispiel konstruieren, bei dem Median grösser als Mittelwert ist.
- Eine erhobene Grösse ersinnen, bei der Median (oder ein anderes Quantil) mehr interessiert als der Mittelwert und umgekehrt.
Boxplot
 Ein Boxplot besteht aus einer Box, welche durch das erste und dritte Quartil ($Q_{25\%}$ und $Q_{75\%}$) begrenzt ist. Damit liegen $50\%$ der Daten in der Box. Der mittige Strich ist der Median ($q_{50\%}$), die Whiskers (Antennen oder Schnäuze) sind $w_1=Q_{50\%}-1.5\cdot IQA$ und $w_2=Q_{50\%}+1.5\cdot IQA$. $w_1$ und $w_2$ sind dabei zum Teil auch durch den grössten (resp. kleinsten für $w_1$) Wert eines Datenpunktes ersetzt, welcher gerade noch kleiner (resp. grösser für $w_1$) ist als $w_2$. Die Whiskers sind dann nicht symmetrisch. Die Punkte, die ausserhalb der Whiskers liegen, nennt man Outlier oder Ausreisser. Man kann zeigen, dass bei normalverteilten Daten, ca. $95\%$ der Beobachtungen innerhalb der beiden Whiskers zu liegen kommen.
Ein Boxplot besteht aus einer Box, welche durch das erste und dritte Quartil ($Q_{25\%}$ und $Q_{75\%}$) begrenzt ist. Damit liegen $50\%$ der Daten in der Box. Der mittige Strich ist der Median ($q_{50\%}$), die Whiskers (Antennen oder Schnäuze) sind $w_1=Q_{50\%}-1.5\cdot IQA$ und $w_2=Q_{50\%}+1.5\cdot IQA$. $w_1$ und $w_2$ sind dabei zum Teil auch durch den grössten (resp. kleinsten für $w_1$) Wert eines Datenpunktes ersetzt, welcher gerade noch kleiner (resp. grösser für $w_1$) ist als $w_2$. Die Whiskers sind dann nicht symmetrisch. Die Punkte, die ausserhalb der Whiskers liegen, nennt man Outlier oder Ausreisser. Man kann zeigen, dass bei normalverteilten Daten, ca. $95\%$ der Beobachtungen innerhalb der beiden Whiskers zu liegen kommen.
Geogebra kann mit Hilfe von Ansicht → Tabelle → Daten eingeben → Analyse einer Variable → Boxplot Boxplot-Grafiken erstellen. In Excel ist es auch möglich, allerdings etwas mühsamer.
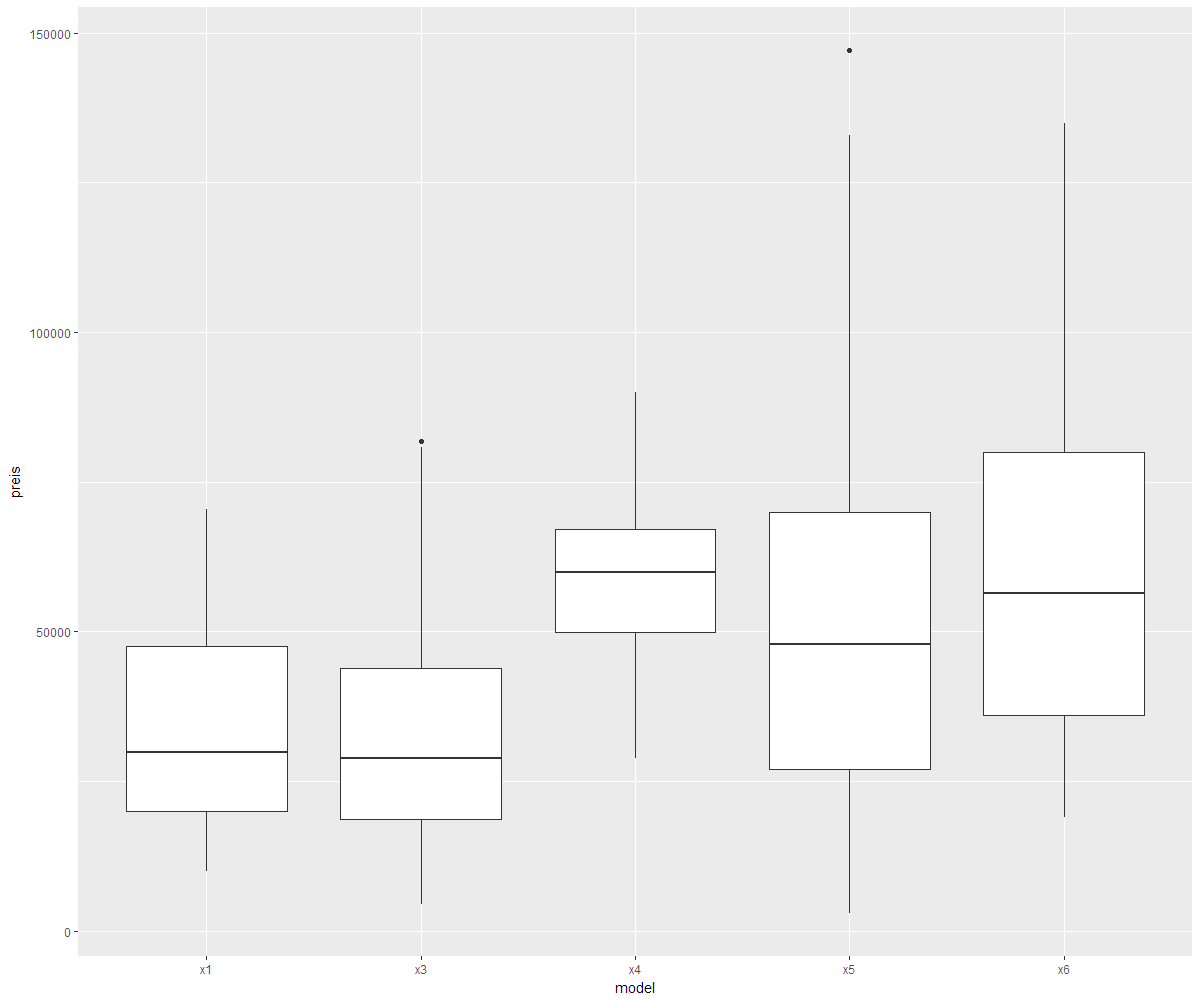
Boxplot der Preise nach Modell
Interpretation Boxplot
Lektion 06
Ziele
- Boxplots Verteilungen zuordnen können
- Anwendungen von Boxplots und Quantilstatistiken kennen
- Lorenzkurve kennen / interpretieren können
Aufträge
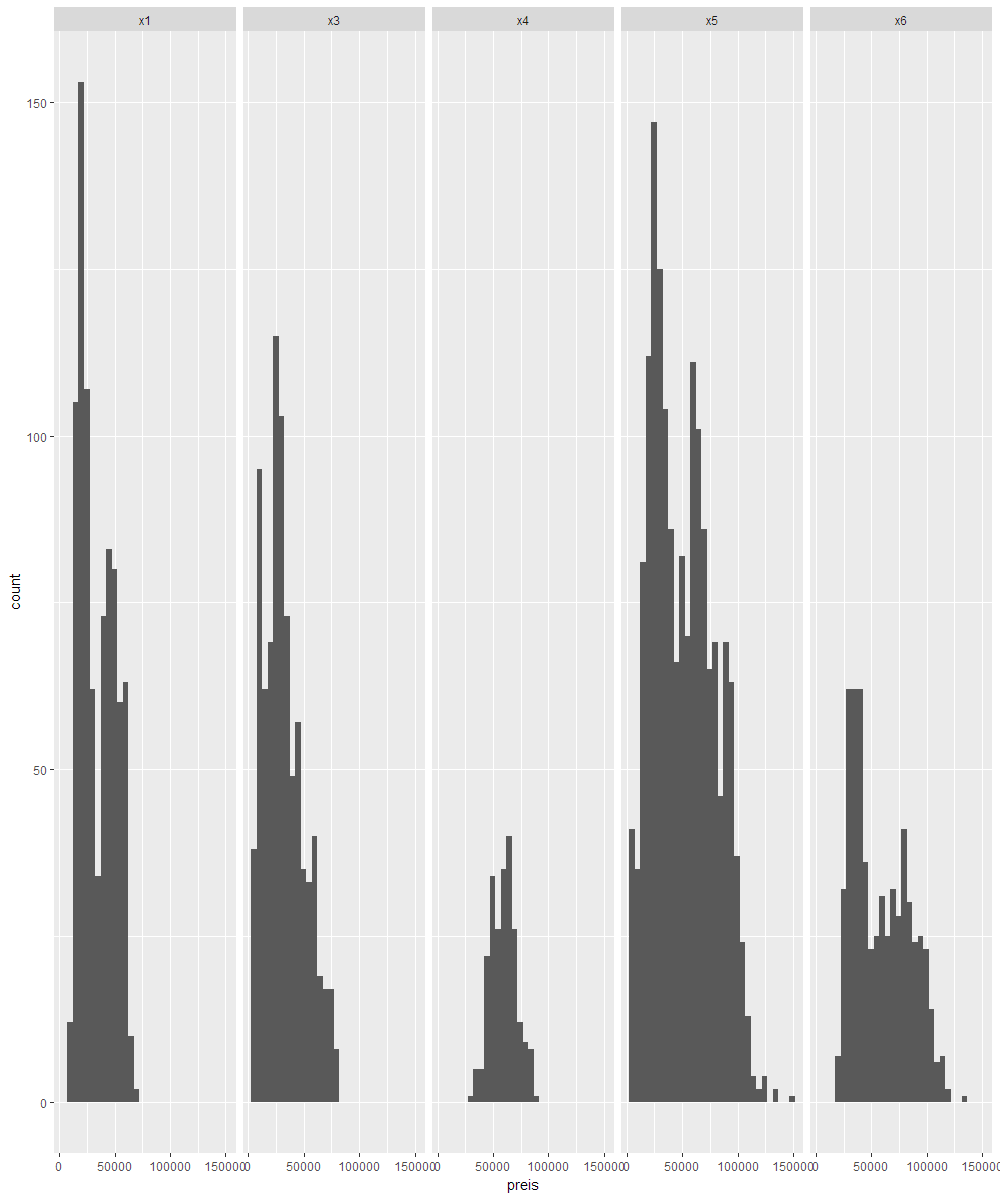
- Zuordnen der Kennzahlen (Variante 1,2,3) auf Histogramme:
- Variante 1: Jede Kennzahl und Modelle sind beliebig durcheinander
- Variante 2: Die Modelle sind spaltenweise vertauscht. In einer Spalte stehen aber nur Kennzahlen zu gleichen Modell.
- Zuordnen von Boxplots auf Histogramme: Jeder Boxplot wird einem Histogramm zugeordnet.
- Lorenzkurve
- Theorie Lorenzkurve lesen
- Beispiel mit Hilfe der Excel-Datei zur Lorenzkurve erstellen, die maximal ungleich verteilt sind resp. gleich verteilt sind
- Eine Lorenzkurve für die Preise der BMW X5 in Excel-Datei erstellen.
- Artikel zur Lorenzkurve lesen und Seiten 14-16 in Lohnreport der Stadt Zürich betrachten. Überrascht die Grafik? Wie sähe die Verteilung in der Stadt St. Gallen aus?
- Auf der OECD-Webseite können verschiedene Merkmale zur Einkommensverteilung über die Zeit (Schiebregler unten rechts) für verschiedene Länder betrachtet werden. Suche dir ein Land, dessen Gini-Koeffizient sich in den letzten Jahren stark verändert hat. Was könnte eine Geschichte dazu sein?
- Überlege dir alternative Masse, um Konzentration resp. Ungleichverteilung (im Einkommenskontext) zu messen.
Theorie
Auf Grund der Lorenzkurve kann ausgesagt werden, wie stark die Merkmale (resp. deren Ausprägung) konzentriert sind (ein Konzentrationsmass). Das klassische Beispiel dabei ist die Einkommenverteilung. Die Frage, die dabei gestellt, resp. beantwortet wird, ist “Wie viel Prozent der Leute (Köpfe) verdienen wie viel Prozent des Gesamteinkommens?»
| Einkommen | Anzahl Personen | Kumululierte relative Anzahl | Einkommenssumme | Kumululierte relative Einkommenssumme |
|---|---|---|---|---|
| 2317 | 10 | 0.20 | 23'170 | 0.17 |
| 2552 | 11 | 0.42 | 28'072 | 0.37 |
| 2787 | 14 | 0.70 | 39'018 | 0.65 |
| 3022 | 8 | 0.86 | 24'176 | 0.83 |
| 3257 | 3 | 0.92 | 9'771 | 0.90 |
| 3492 | 4 | 1.00 | 13'968 | 1.00 |
| Total | 50 | 138'175 | ||
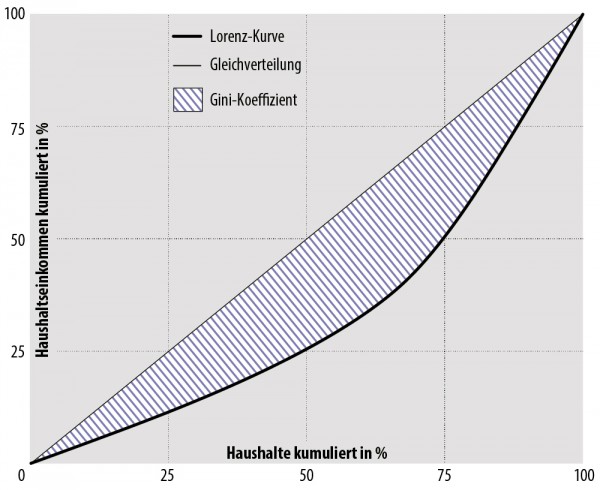
Zeichnet man nun die Punkte $(\text{Kumulierte relative Anzahl},\text{Kumulierte relative Einkommenssumme})=(x,y)$ und verindet diese, erhält man die Lorenzkurve:
 Würden alle gleich viel verdienen, lägen die Punkte auf der Winkelhalbierenden.
Würden alle gleich viel verdienen, lägen die Punkte auf der Winkelhalbierenden.
Als Mass der Ungleichverteilung verwendet nun die Fläche, welche die Lorenzkurve mit der Winkelhalbierenden einschliesst. Diese Fläche nennt man auch Gini–Koeffizient
Als Beispiel für die Lorenzkurve wiederum die 5 BMW Modelle und ihre Preise. Achtung: Es handelt sich dabei nicht um ein Einkommen!
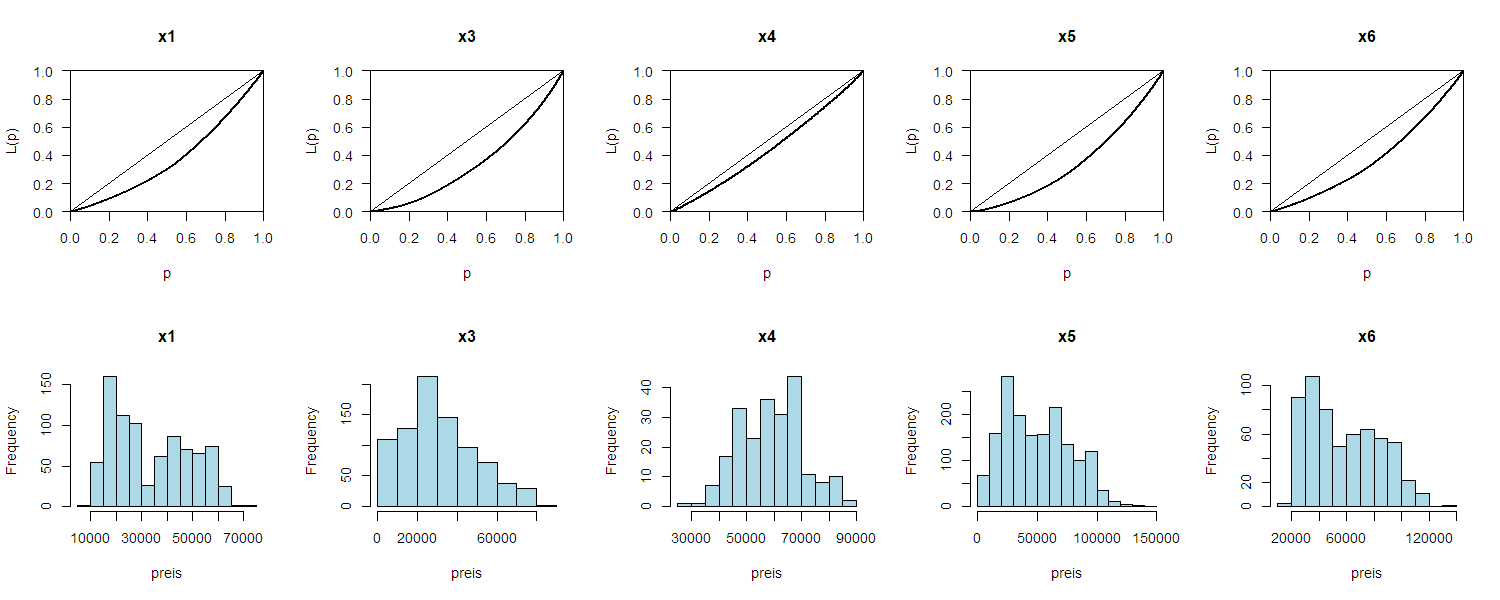
Die Lorenzkurve macht im Allgemeinen nur Sinn für Merkmale, mit positiven Werten (Preis, Einkommen, etc.)
Lektion 07
Ziele
- Jede/r kann die $Z$-transformierte (standardisierte) eines Merkmals ausrechnen.
- Jede/r kann auf Grund von Histogrammen der $Z$-transformierten Merkmale entscheiden, ob ein Merkmal normalverteilt ist.
- Jede/r kann die Wahrscheinlichkeit berechnen, dass ein Merkmal innerhalb / ausserhalb eines Intervalls zu liegen kommt.
Aufträge
- Theorie durchlesen
- Für die Variablen aus der Excel-Datei zu Geburtsgewicht, Autopreise und Aktienrenditen jeweils
- standardisieren in einer weiteren Spalte
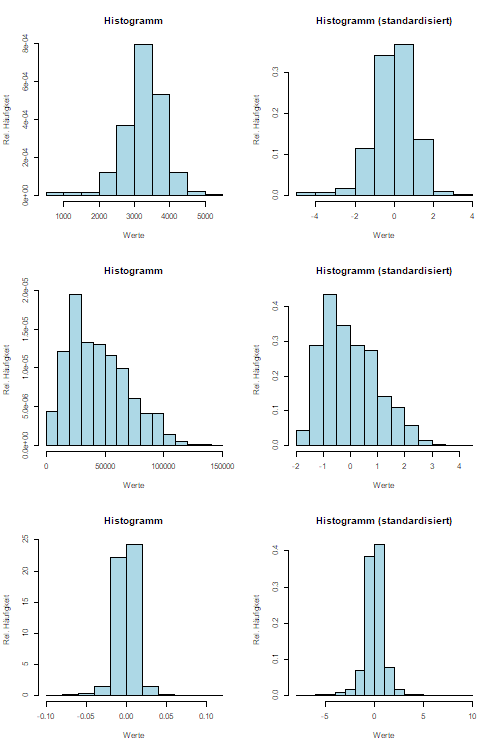
- zwei Histogramme erstellen: Eines vor und eines nach der Standardisierung (z.B. mit Geogebra)
- entscheiden, ob die Variable normalverteilt ist oder nicht.
- Für die normalverteilten Variablen ein Intervall der Form $[a,b]$ angeben, in welchem $95\%$ der Daten zu liegen kommen.
Theorie
Normalverteilung
Grosse Teile der Statistik beruhen auf der sogenannten Normaleverteilung. Eine Grösse resp. ein Merkmal ist normalverteilt, wenn die Ableitung der Verteilungsfunktion durch $f(x)=\frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}}$ gegeben ist. Für unsere Zwecke erscheint das aber kryptisch und wir beschränken uns darauf, festzuhalten, dass ein Histogram einer Standard-Normalverteilten Zufallsvariable wie folgt aussieht:
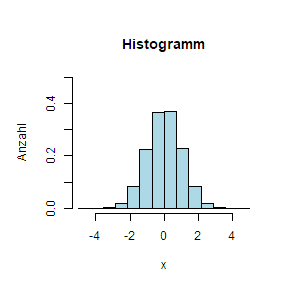
Aussehen Normalverteilung
Dabei ist wichtig festzuhalten, dass die Anzahl der Klassen in Histogramm offensichtlich willkürlich ist. Der theoretische Unterbau besagt aber, dass die Klassen beliebig klein gewählt werden können und das Histogramm zum Schluss (bei unendlich kleiner Klassenbreite und unendlich vielen Beobachtungen) dem Graphen der Funktion $f$ von oben entspricht.
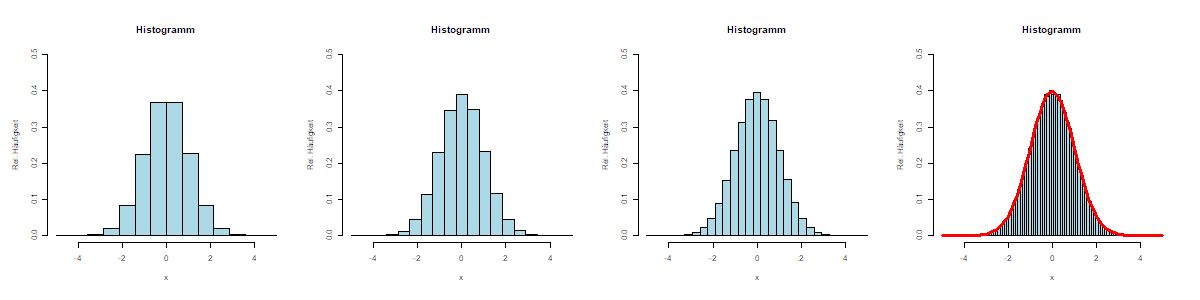
Standardnormalverteilung und Standardisieren
Um nun sicher zu stellen, dass man immer von der gleichen Normalverteilung spricht, transformiert man Merkmale. Wenn $\mu_X=\frac1n\sum_{i=1}^n x_i$ und $\sigma_X=\sqrt{\frac1{n-1}\sum_{i=1}^n}$ ist, dann sagt man, dass das Merkmal $Z=\frac{X-\mu}{\sigma}$ das standardisierte Merkmal von $X$ ist. Man kann dann jede Beobachtung $x_i$ zu $z_i=\frac{x_i-\mu}{\sigma}$ standardisieren.
| $x_i$ | $x_i-\mu_X$ | $\frac{x_i-\mu_X}{\sigma_X}$ | |
|---|---|---|---|
| -5 | -9 | -1.21 | |
| 5 | 1 | 0.13 | |
| 5 | 1 | 0.13 | |
| 0 | -4 | -0.54 | |
| 15 | 11 | 1.48 | |
| $\mu$ | 4 | 0 | 0 |
| $\sigma$ | 7.41 | 7.41 | 1 |
Berechnet man nun den Mittelwert von $Z$, $\mu_Z$ und die Standardabweichung von $Z$, $\sigma_Z$ so kommt – egal wie $X$ ursprünglich verteilt ist – heraus, dass $\mu_Z=1$ und $\sigma_Z=1$ ist.
Ist nun ein Merkmal $X$ *normalverteilt* so ist das standardisierte Merkmal *standardnormalverteilt*, das heisst, es ist normalverteilt Standardabweichung $\sigma=1$ und Mittelwert $\mu=0$.
Wahrscheinlichkeiten
Für standard-normalverteilte Merkmale – und damit auch für normalverteilte Merkmale – können sehr starke Aussagen über die Verteilung gemacht werden. So gilt z.B., dass im Intervall $[\mu_X-\sigma_X,\mu_X+\sigma_X]$ $68\%$ der Daten liegen. Für andere Vielfachen gilt die Tabelle unten:
| n | Prozent in $[\mu_x-n\cdot\sigma_X,\mu_x+n\cdot\sigma_X]$ | |
|---|---|---|
| 1 | $68.3\%$ | |
| 2 | $95.4\%$ | |
| 3 | $99.7\%$ | |
| 4 | $\approx 100\%$ |
Hat ein normalverteiltes Merkmal zum Beispiel den Mittelwert $\mu_X=11.2$ und $\sigma_X=3.1$ dann liegen ca. $68\%$ der Daten im Intervall $[8.1,14.3]=[11.2-3.1,11.2+3.1]$, das heisst in einem Intervall der Breite zwei $\sigma$ zentriert um den Mittelwert liegen ca. $68\%$ der Daten.
Relevanz
Der Begriff einer (Standard-)normalverteilten Variable ist sehr wichtig: Einerseits, weil theoretisch gezeigt werden dann, dass die Summe vieler gleichartiger und unabhängiger Zufälle immer normalverteilt ist und andererseits weil eben gerade die Eigenschaft dazu führt, dass viele Daten in der “Welt da draussen” normalverteilt sind.
Aus einer mathematischen Sicht gilt noch anzumerken, dass zum Teil auch der Logarithmus eines Merkmals normalverteilt sein kann. Dies ist dann der Fall, wenn davon auszugehen ist, dass das Merkmal das Produkt vieler gleichartigen und unabhängigen Zufällen ist.
Daten in R
#Daten aus Clipboard
inputdata <- read.table(file("clipboard"), sep="\t") #returns dataframe from excel clipboard separated by tab
#oder
inputdata <- readClipboard(file("clipboard")) #if single column
#oder
inputdata <- read.csv2("filenname.csv") #separation by semicolon
Lektion 08
Ziele
- Jede/r kann einen Scatterplot von zwei Datenreihen / Merkmalen erstellen
- Jede/r kann die Korrelation von zwei Datenreihen / Merkmalen berechnen
- Jede/r kann die Korrelation interpretieren und die Masszahl Punktewolken aus dem Scatterplot zuordnen.
Auträge
- Lies die Theorie unten durch.
- Korrelation im Auto-Datensatz
- Wähle ein BMW-Modell und erstelle eine Scatterplott, wobei der Preis auf der $y$-Achse ist und eine erklärende Variable auf der $x$-Achse ist. Was wären sinnvolle Variablen für die $x$-Achse, für welche du einen Zusammenhang mit dem Autopreis vermutest?
- Berechne die Korrelation und das Bestimmtheitsmass für die gewählten Variablen.
- Welche Korrelationen (Vorzeichen und Stärke) vermutest du im Datensatz? Welche zwei Variablen sind jeweils wie korreliert?
- Schau dir die Webseite Tylver Vigen an: Wähl dir das widersinnigste Beispiel. Gibt es eine Erklärung dafür? (Die aktuelle Version dieser Webseite ist schöner, allerdings ohne Tabellen)
Theorie
Wird ein Zusammenhang zwischen zwei kardinalen Merkmalen vermutet, sollte als erstes ein sogenannter Scatterplot erstellt werden. Zu diesem Zweck, wird das eine Merkmal auf der $x$-Achse und das andere Merkmal auf der $y$-Achse abgetragen.
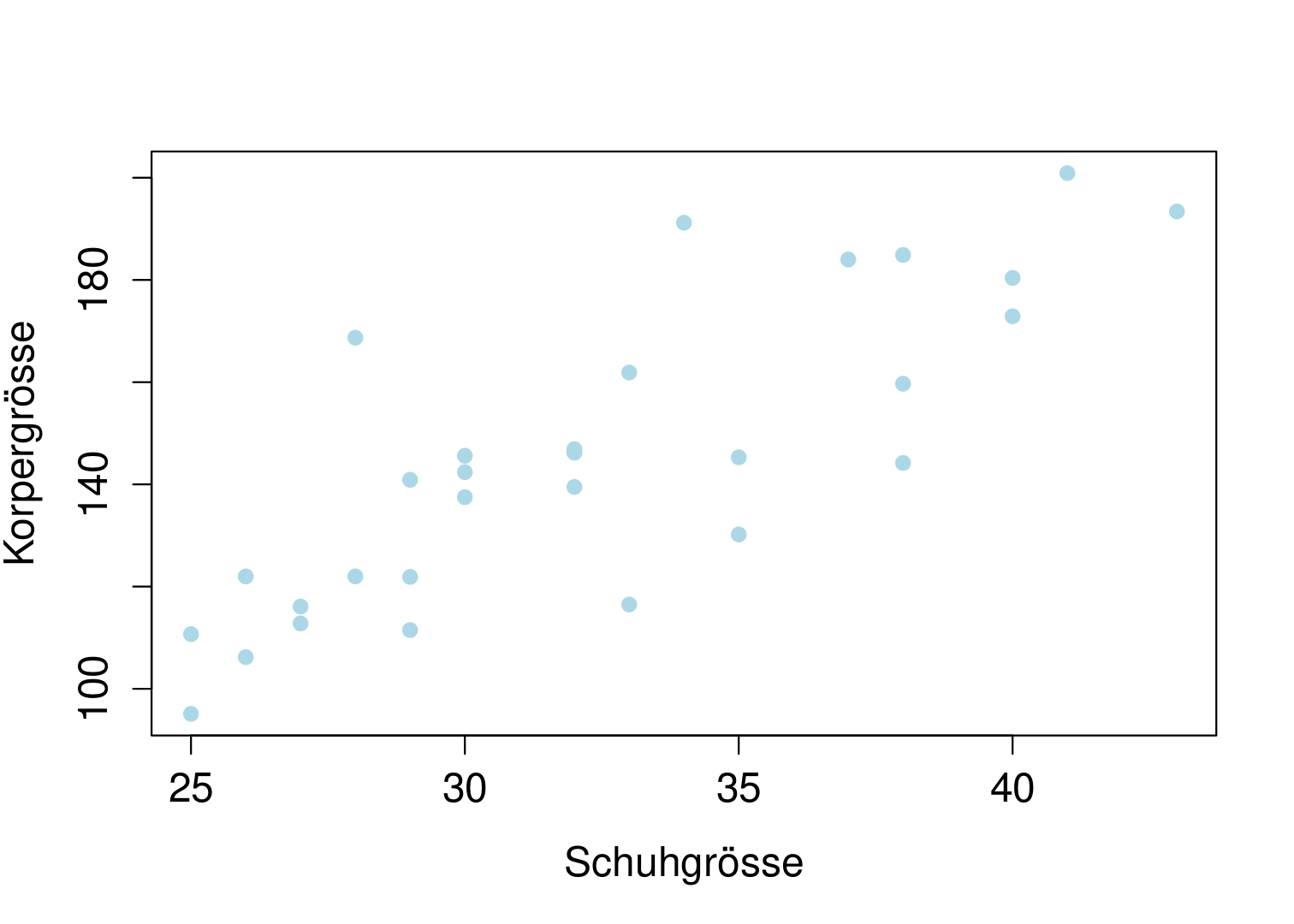
Nun gibt es ein Mass für diesen Zusammenhang: Die Stärke wie auch die Richtung des Zusammenhangs der Mermkale $X$ und $Y$, $R_{xy}$, wird mit der Korrelation gemessen: $$R_{xy}=\frac{\sum\limits_{i=1}^n (x_i-\bar{x})(y_i-\bar{y})}{\sqrt{\sum\limits_{i=1}^n (x_i-\bar{x})^2 \sum\limits_{i=1}^n (y_i-\bar{y})^2}}$$ Die Korrelation nimmt nur Werte zwischen $-1$ und $1$ an. In Excel wie auch in R sind Funktionen zur Berechnung der Korrelation hinterlegt. Wichtig dabei ist zu beachten, dass die Korrelation nur einen linearen Zusammenhang misst:
 Möchte man die Stärke der Korrelation messen, quadriert man $R_{xy}$ zur $R^2=R_{xy}^2$. Man spricht von einem «starken Zusammenhang» wenn $0.5\leq R^2\leq 1$ ist, von einem «moderaten Zusammenhang» wenn $0.25\leq R^2 < 0.5$ ist, und schliesslich von einem «schwachen Zusammenhang» wenn $0.1\leq R^2<0.25$ ist. Ist schliesslich $R^2$ kleiner so liegt kein Zusammenhang vor. $R^2$ wird auch Bestimmtheismass genannt.
Möchte man die Stärke der Korrelation messen, quadriert man $R_{xy}$ zur $R^2=R_{xy}^2$. Man spricht von einem «starken Zusammenhang» wenn $0.5\leq R^2\leq 1$ ist, von einem «moderaten Zusammenhang» wenn $0.25\leq R^2 < 0.5$ ist, und schliesslich von einem «schwachen Zusammenhang» wenn $0.1\leq R^2<0.25$ ist. Ist schliesslich $R^2$ kleiner so liegt kein Zusammenhang vor. $R^2$ wird auch Bestimmtheismass genannt.
Zusammenfassend kann gesagt werden, dass Richtung und Stärke eines linearen Zusammenhangs gemessen werden kann:
- Richtung: Eine positive Korrelation beschreibt eine «je-mehr-desto-mehr» Beziehung, eine negative Korrelation beschreibt eine «je-weniger-desto-mehr» Beziehung.
- Stärke: Um nur eine Aussage über die Stärke des Zusammenhangs unabhängig der Richtung zu machen, verwendet man das Bestimmtheitsmass $R^2$, die quadrierte Korrelation.
Korrelation und Kausalität
Auch wenn $R^2$ sehr gross ist, muss das nicht heissen, dass in Tat und Wahrheit wirklich ein Zusammenhang dieser beiden Variablen vorliegt. Es kann durchaus sein, dass die Korrelation zufällig zu Stande gekommen ist. Man spricht dann auch von Scheinkorrelation oder in Englisch von spurious correlation.
Kausalität in diesem Zusammenhang besagt, dass ein Merkmal ein anderes bedingt: So ist zum Beispiel bei der Thematik Schuhgrösse und Körpergrösse wirklich davon auszugehen, dass ein kausaler Zusammenhang besteht.
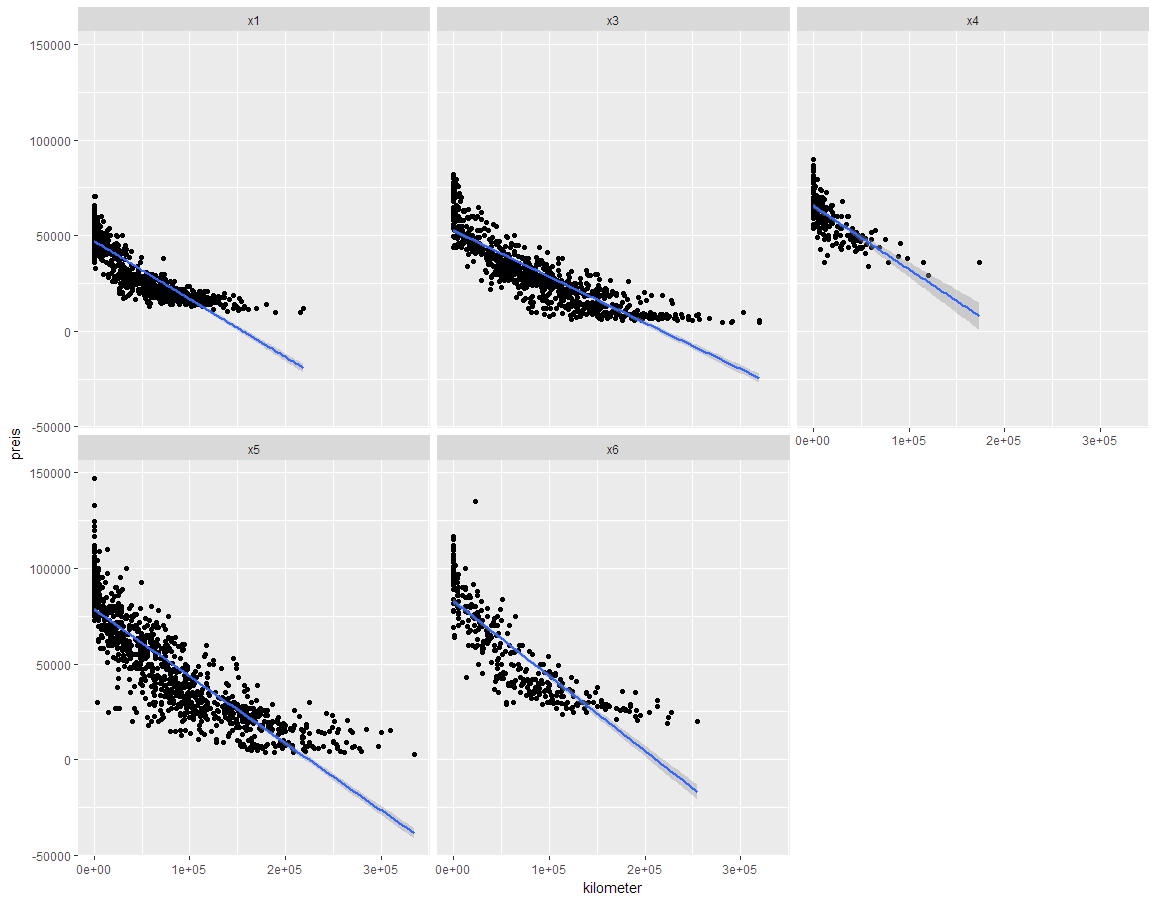
Korrelationen BMW Datensatz nach Modell
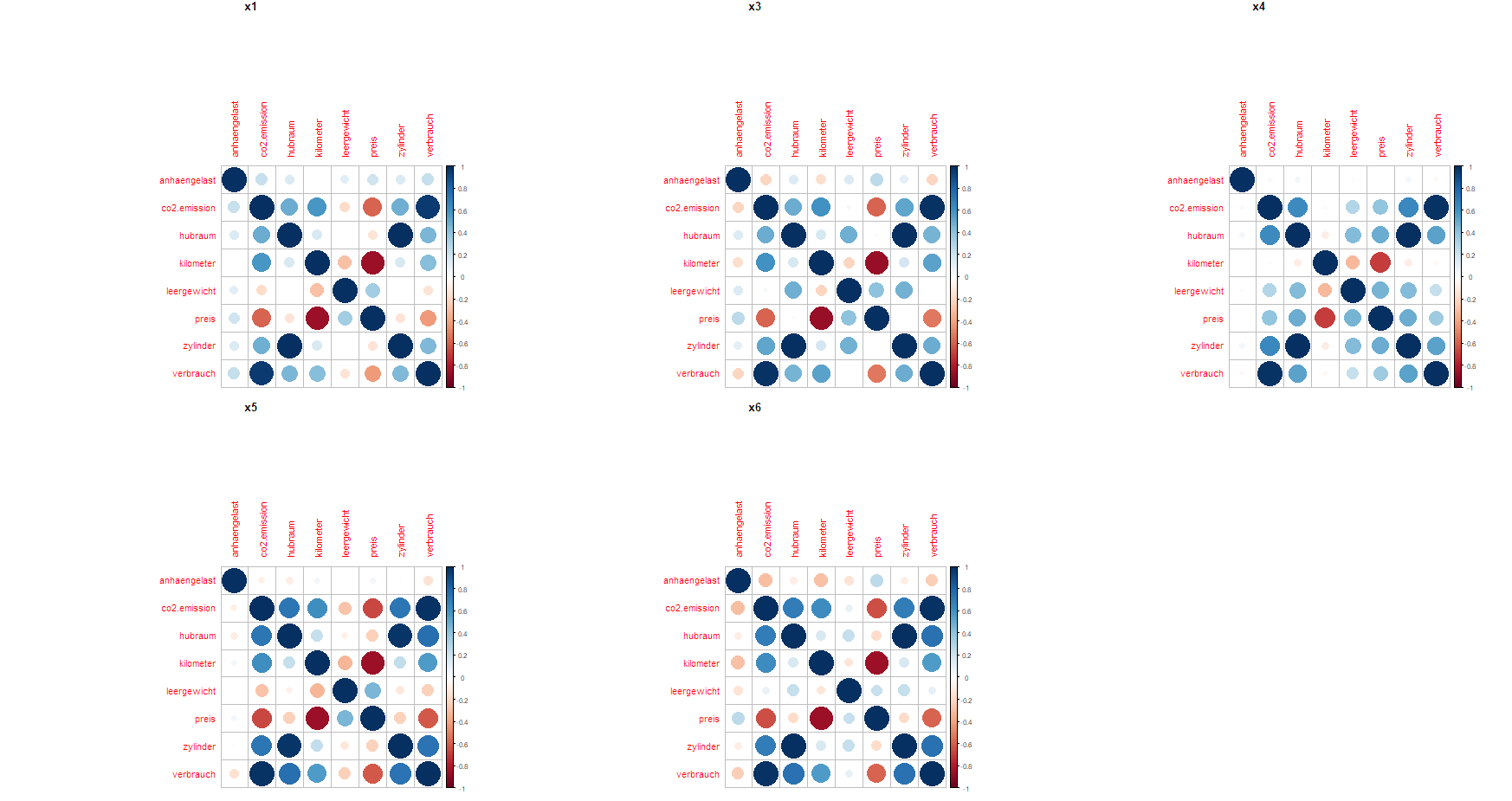
Lektion 09
Ziele
- Jede/r kann eine eindimensionale Regression mit Excel durchführen und interpretieren.
- Jede/r kann das Problem (mathematisch) formulieren, dessen Lösung die Ausgleichsgerade ist.
- Jede/r kann eine Schätzung abgeben, wie viel ein gefahreren Kilometer gemäss dem eigenen Regressionsmodell kostet
Aufträge
- Theorie Regression
- Theorie Regression unten durcharbeiten
- Demo-Video zur Durchführung Regression in Excel anschauen
- Praxis Regression:
- Regression auf den beiden Tabellenblättern (Bsp 1 und Bsp 2) in der Datei zur heutigen Lektion durchführen.
- Scatterplot erstellen
- Regression durchführen, Geradengleichung aufstellen und Koeffizienten interpretieren.
- Mögliche Fragen:
- Wie lautet die Gleichung der beiden Geraden?
- Welche Gerade ist «besser»?
- Regression für ein BMW-Modell durchführen
- Eine Regression durchführen, bei der der Preis auf die gefahrenen Kilometer regressiert wird. Modell (Geradengleichung) aufstellen und «Kosten» eines Kilometers (von 1000 Kilometern) angeben.
- Freiwillig: Anstelle des Preises kann auch der Logarithmus des Preises als $y$-Variable verwendet werden. Wird das Modell ($R^2$) besser oder schlechter? Was heisst das für die Interpretation?
Theorie
Bei der Regression geht es letztendlich darum, den Zusammenhang, der in der letzten Lektion mit der Korrelation beobachtet worden ist, genauer zu beschreiben.
Die Idee der Regression ist, die Summe der quadratischen Abstände einer Geraden zu den beobachteten Datenpunkten zu minimieren. Dabei ist wichtig zu beachten, dass nur die vertikalen Abstände betrachtet werden:
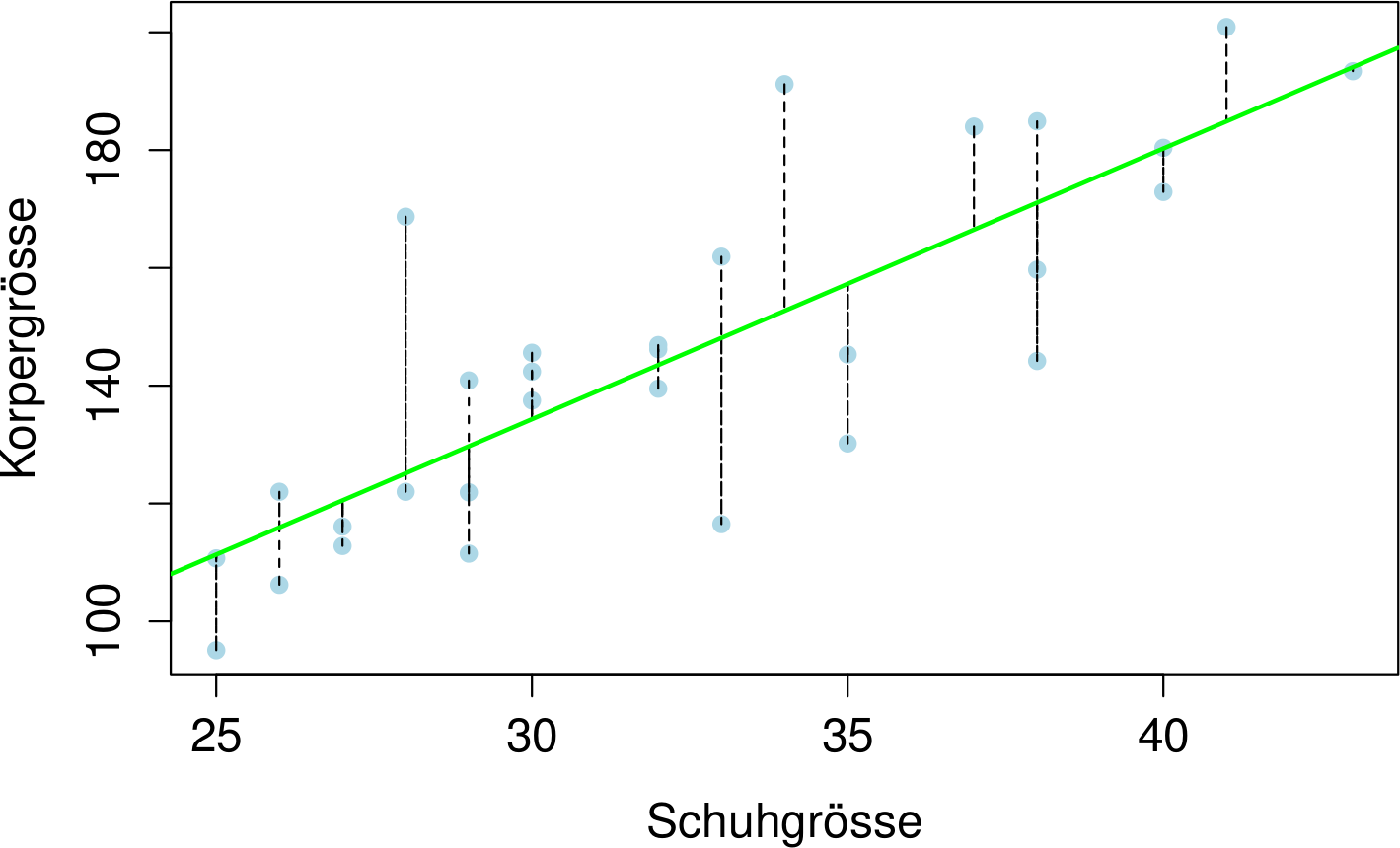
Jede lineare Funktion $g$ kann als $g:y=mx+q$ beschrieben werden. Man sucht also $m$ und $q$ so, dass die quadrierte Summe der Längen der gestrichelten Linien minimal ist.
Streng mathematisch ausgedrückt hat man die Wertepaare $(x_1,y_1),\, (x_1,y_1),\,(x_3,y_3), \ldots,(x_n,y_n)$. Hat man nun einen beobachtete $x$-Wert $x_i$ so ist die Vorhersage der Gerade für den $y$-Wert $mx_i+q$. Für ein gegebenes $m$ und $q$ ist damit der Abstand des $i$-ten Datenpunktes also $y_i-(mx_i+q)$, entsprechend ist der quadrierte Abstand des $i$-ten Datenpunktes $y_i-(mx_i+q))^2$.
Schliesslich sucht man eben $m$ und $q$ so, dass die Summe $$ (y_1-(mx_1+q))^2+(y_2-(mx_2+q))^2+(y_3-(mx_3+q))^2+\cdots (y_n-(mx_n+q))^2=\sum_{i=1}^n (y_i-(mx_i-q))^2 $$ minimal ist.
Betrachtet man diese Summe genauer, stellt man fest, dass dieser Ausdruck ein quadratischer Ausdruck ist, wenn man $m$ und $q$ als Variablen betrachtet. In anderen Worten, würde man – für gegebene Datenpunkte werden $x_i$ und $y_i$ zu Zahlen – diesen Ausdruck als Graph darstellen, erhielte man eine Parabel. Für Parabeln kann der Scheitelpunkt, welcher das Minimum der Parabel ist, einfach mit der Scheitelpunktformel berechnet werden.
Mit dieser Feststellung kann dann $m= \frac{\sum\limits_{i=1}^n (x_i - \bar x)(y_i - \bar y)}{\sum\limits_{i=1}^n (x_i - \bar x)^2}$ und $q=\bar y-m\bar x$ berechnet werden. Die Berechnung von $m$ und $q$ mit diesen Formeln führt zum Ziel, ist aber umständlich. Alle vernünftigen Datenanalyse-Programme können sogenannte Regressionsanalysen – oder eben Ausgleichsgeraden – berechnen.
Lösungen
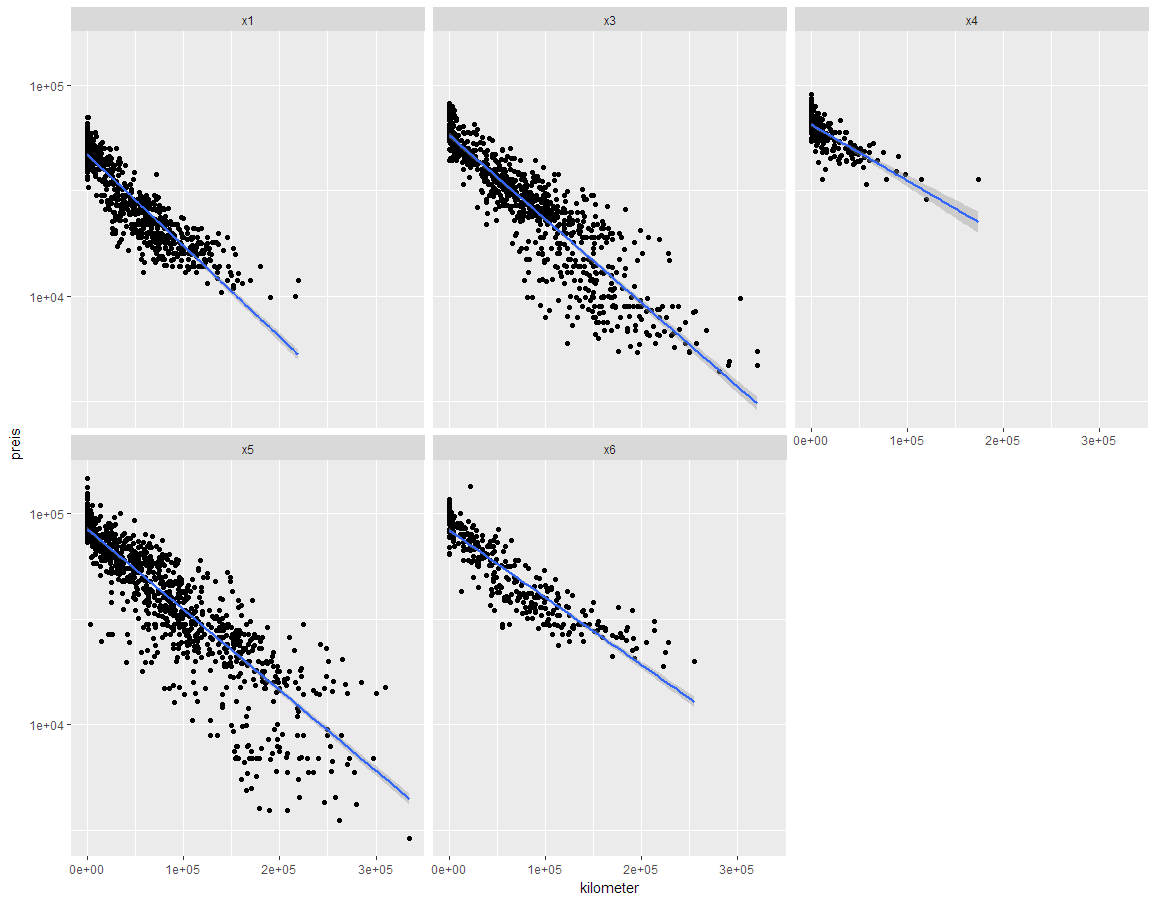 Berechnet man für die normalen Preise (nicht $\log$) die Regressiongerade, erhält man:
Berechnet man für die normalen Preise (nicht $\log$) die Regressiongerade, erhält man:
- x1: $y = -0.3029\cdot x+47132$
- x3: $y = -0.2412\cdot x+52607$
- x4: $y = -0.3317\cdot x+65518$
- x5: $y = -0.35\cdot x+78561$
- x6: $y = -0.3912\cdot x+82847$
Für den X1 «kostet» also ein gefahrener Kilometer ca. 30 Rp, für den X6 kostet dieser ca. 39 Rp
Lektion 10
Ziele
- Jede/r kann die Regression von letzten Mal mit und ohne Logarithmus des Preis korrekt interpretieren
- Multivariate Regression
- Jede/r kann eine multivariate Regression mit Excel oder R durchführen.
- Jede/r kann die Koeffizienten von kardinalen und optional Dummy-Variablen einer multivariaten Regression interpretieren.
Autrag
- Modell vom letzten Mal in normaler (Variante 1) und logarithmischer Spielweise (Variante 2) nochmals durchrechnen. Die Koeffizienten in beiden Modellen interpretieren und als Satz (!!!) festhalten.
- Gefahrene Kilometer für ein BMW Model auf Alter regressieren. Wie ist der Koeffizient ($m$) vom Alter zu interpretieren?
- Theorie Teil I unten durcharbeiten und durchlesen
- Multivariate Regression des Preises mit Kilometer und Alter durchführen für ein Auto-Modell
- Theorie Teil II unten durcharbeiten.
- Multivariate Regression mit Kilometer, Alter und einem beliebigen Dummy (Farbe Rot, Unfall, Getriebe-Art, etc.) durchführen.
- Plausibilität der erhaltenen Modelle / Koeffizienten mit dem Partner besprechen und auf Plausibilität überprüfen.
Daten Lektion 10
Für diese Lektion sind den ursprünglichen Daten mehrere Kolonnen (Alter in Tagen, Alter in Jahren, Diesel Ja) hinzugefügt worden, die in dieser Lektion zu verwenden sind. Diese finden sich hier als Excel-Datei.
Theorie
Teil 1
Beim letzten Mal haben wir die univariate Regression besprochen. Dabei geht es darum eine Variable ($Y$, Preis) auf eine andere Variable ($X$, Kilometer) zu regressieren. Zum Schluss haben wir ein Modell erhalten, dass einen Zusammenhang der Form \[ Y=q+m\cdot X \] beschreibt. Man sagt auch $Y$ ist die abhängige Variable, $X$ die erklärende Variable.
Man könnte jetzt noch weiter gehen und eine Variable ($Y$, Preis) auf mehrere andere Variablen ($X_1$, Kilometer; $X_2$, Alter) regressieren. Das Modell in diesem Fall würde dann lauten: \[ Y=q+m_1\cdot X_1 + m_2\cdot X_2. \] Der Preis ($Y$) ist dann also eine lineare Funktion der gefahrenen Kilometern ($X_1$) sowie des Alters ($X_2$).
Man kann diese Überlegung nun auf beliebig viele erklärende Variablen ausweiten um ein allgemeines Modell mit $k$ Variablen der Form \[ Y=q+m_1\cdot X_1 + \cdots+m_k\cdot X_k \] zu erhalten. Die Idee ist dabei dieselbe wie bei der univariaten Regression (Lektion 09): $q$, $m_1\ldots,m_k$ werden so bestimmt, dass die Summe der quadratischen Abweichungen der Modellvorhersage vom beobachteten Wert minimal ist. Die Werte $q$, $m_1\ldots,m_k$ heissen auch Koeffizienten. In statistischen Kontext verwendet man dafür auch oft die Buchstaben $\beta$: Es ist dann $\beta_0=q$ und $\beta_i=m_i$.
Teil 2
Alle bisher betrachteten Variablen waren kardinaler Natur (Preis, Kilometer, Verbrauch, etc.). Möchte man nun nominale Variablen als erklärende Variablen verwenden (z.B. Farbe, Getriebeart, Treibstoff etc.) so muss man diese erst in sogenannte Dummy-Variablen umwandeln.
Für den Treibstoff könnte man unterscheiden zwischen «Diesel» und «Nicht Diesel»: Man kreiert also eine neue Variable diesel_ja welche den Wert $1$ annimmt, wenn das Fahrzeug mit Diesel ist und $0$ sonst. Damit ist dann der Wert des zur Variable diesel_ja gehörenden Koeffizienten, eben genau dieser Betrag, um welcher der Preis erhöht wird, wenn das Auto mit Diesel fährt. Genau gleich kann man mit allen nominalen Variablen verfahren, die zwei Ausprägungen haben (z.B. Schaltung/Manuell, Unfall/kein Unfall, etc.)
Für Variablen, die mehr als zwei Ausprägungen haben. Man erstellt in diesem Fall einfach mehrere Dummy-Variablen. Z.B. könnte man um die Farben rot, grün, blau in einer Regression folgende zwei Dummy-Variablen berüchichtigen um dann die ursprünglichen Farben zu codieren
rot_ja | grün_ja |
|
|---|---|---|
| rot | 1 | 0 |
| grün | 0 | 1 |
| blau | 0 | 0 |
Der Koeffizient von rot_ja ist dann die Preisdifferenz eines roten Autos; der Koeffizient von grün_ja ist die Preisdiffernez eines grünen Autos. Offensichtlich wird dabei immer die Preisdifferenz zu einem Basisauto angenommen, welches im Fall der obigen Codierung blau ist.
Um eine Nominale-Variable mit $n$ Ausprägungen zu codieren, braucht man also $n-1$ Dummy-Variablen.
Durchführung
Excel kann genau gleich wie univariate Regression auch multivariate Regression durchführen. Für die Beispieldaten könnte ein Modell, welches Preis auf die Variablen Alter, Kilometer, Alter (Jahren) und Verbrauch regressiert, wie folgt über den Assistenten eingegeben werden:
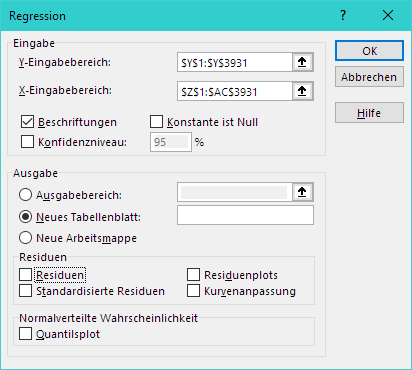
Wichtig dabei ist, dass alle erklärenden Variablen in nebeneinanderliegen Spalten sind (Oben: In den Spalten Z bis AC, für die Zeilen 1 [Titel] bis 3931).
Caveat: Excel ist nicht die optimale Lösung für solche Probleme. Dies äussert sich auch in z.T. ungenauen / falschen Berechnungen. Für weiterführende Zwecke, sollte ein Statistikprogramm verwendet werden.
Lektion 11
Ziele
- Jede/r kann die Begriffe «Modellwelt» (Wahrscheinlichkeit, theoretisch) und «Beobachtete Welt» (Statistik, beobachtet) einordnen und umgangssprachlich erklären
- Jede/r kann den Begriff «Binomialverteilung» umgangssprachlich erklären und die theoretische Wahrscheinlichkeit berechnen, dass ein gewisses Phänomen eine bestimmte Anzahl mal auftritt
- Optional: Jede/r kann den Begriff «Normalverteilung» umgangssprachlich erklären
Autrag
- Dem Lehrer zuhören und anschliessend die Wandtafel photografieren.
- Experimente (Statistik) versus Theorie (Wahrscheinlichkeit)
- Wirf eine Münze $n$ mal und zähle (
ANZAHL()) die Anzahl Male «Kopf». Berechne auch die durchschnittliche Anzahl Kopf pro Wurf. Wie ist dieser Durchschnitt in der «Modellwelt» zu interpretieren? - Wirf drei Münzen $n$ Mal gleichzeitig und zähle jeweils die Anzahl «Zahl». Fertige ein Histogramm an.
- Berechne mit Excel die theoretischen Wahrscheinlichkeiten für eine Binomialverteilung (drei Münzen, $0$, $1$, $2$, $3$ mal Zahl) und vergleiche diese Werte mit dem Histogramm aus der vorigen Aufgabe
- Jemand hat 100 mal eine Münze geworfen. Wie gross ist die theoretische Wahrscheinlichkeit, dass man genau 67 mal Kopf beobachtet? Nimm an, dass die Münze ausgeglichen ist.
- Schau dir das Video zur <<Tea Tasting Lady>> an. Überlege dir, welche «Fehlentscheide» enstehen können.
Erklärungen
Die Formel BINOM.VERT kann in Excel verwendet werden, um die Wahrscheinlichkeit zu berechnen bei $n$ Durchführungen eines Experiments genau $k$ mal Erfolg zu haben wobei der Erfolg mit Wahrscheinlichkeit $p$ eintritt. Man muss dann BINOM.VERT(k;n;p; FALSCH) aufrufen. FALSCH ist dabei notwendig, dass man die Wahrscheinlichkeit erhält. Würde WAHR stehen, erhielte man die Summe aller Wahrscheinlichkeiten mit Anzahl Erfolgen kleiner gleich $k$.
In R kann genau das gleiche mit dbinom(k, n, p) erreicht werden.
Lektion 12
Ziele
- Jede/r kann den Begriff «Test» im statistischen Sinne erklären und die Fehler die dabei gemacht werden können benennen.
- Jede/r kann für den ELISA Test angeben, wie gross die Wahrscheinlichkeit eines falschen Resultats ist.
- Optional: Jede/r kann erkären, was ein $t$-Test ist.
Auftrag
- Kurz dem Lehrer zuhören zwecks Repetition vom letzten Mal.
- Theorie durcharbeiten.
- Statistische Tests:
- Wie viele Tassen müssen die Lady erkennen, wenn insgesamt 100 Tassen verkostet würden und das Niveau $3\%$ resp. $5\%$ betragen würde?
- Ein einges Beispiel eines statistischen Tests ersinnen und mit Ks diskutieren
- ELISA-Test (Arbeiten mit Vierfeldertafel)
- Jede/r kann für den ELISA-HIV-Test ausrechnen, wie wahrscheinlich ein falsch-positives Resultat ist, wenn zufällig eine europäische Person den HIV-Elisa-Test durchführt.
- Jede/r kann für den ELISA-HIV-Test ausrechnen, wie wahrscheinlich es ist, bei einem positiven Resultat in Tat und Wahrheit HIV negativ zu sein (Annahme: Prävalenz von Europa).
- Optional: Unterscheiden sich die Preise von roten und weissen BMW X1 signifikant?
Theorie
Ein statistischer Test ist eine Entscheidungsregel, mit der entschieden wird, ob die Modellwelt in einem Zustand ($H_0$) ist oder nicht. Für die «tea tasting lady» ist die Annahme der Modellwelt, dass sie es nicht kann. Dies lässt sich übersetzen zur Aussage, dass die Wahrscheinlichkeit, dass sie eine Tasse richtig erkennt zufällig ist, dass heisst, dass ihre Trefferquote $p=50\%=0.5$ ist, man schreibt für diese Annahme $H_0:p=0.5$. Unter dieser Annahme haben wir nun in der letzten Sitzung berechnet, wie gross die Wahrscheinlichkeit ist, dass sie eine gewisse Anzahl Tassen richtig erkennt.
| Anzahl richtige Tassen | Wahrscheinlichkeit | Kumulierte W'keit |
|---|---|---|
| 0 | 0.0010 | 0.0010 |
| 1 | 0.0098 | 0.0107 |
| 2 | 0.0439 | 0.0547 |
| 3 | 0.1172 | 0.1719 |
| 4 | 0.2051 | 0.3770 |
| 5 | 0.2461 | 0.6230 |
| 6 | 0.2051 | 0.8281 |
| 7 | 0.1172 | 0.9453 |
| 8 | 0.0439 | 0.9893 |
| 9 | 0.0098 | 0.9990 |
| 10 | 0.0010 | 1.0000 |
Ein Test legt nun eine Grösse so fest, auf Grund derer entschieden werden kann, in welchem Zustand sich die Welt befindet. Typischerweise spricht man vom Niveau eines Tests welches per Konvention bei $5\%$ liegt.
Im Beispiel der Tassen sucht man sich also diese Anzahl Tassen, so dass die Wahrscheinlichkeit, sich im Schluss zu täuschen, kleiner als $5\%$ ist.
Die Entscheidungsregel ist also «Hat die Lady mehr als ($\geq 8$) Tassen richtig, kann sie es wirklich». Dass sie acht und mehr Tassen zufällig ($H_0:p=0.5$) richtig tippt, beträgt $1-0.9893=0.0107=1.07\%$
| Modellwelt | |||
|---|---|---|---|
| Ja | Nein | ||
| Beob. Welt | Ja | x | Fehler 2. Art |
| Nein | Fehler 1. Art | x | |
Der Fehler 1. Art ist üblicherweise das, was man kontrolliert und dieser wird mit $\alpha$ notiert. In unserem Beispiel, mit einem Untersuch von $10$ Tassen und einem Entscheid von $8$ Tassen haben wir $\alpha=1.07\%$. Der Fehler 2. Art ist üblicherweise schwieriger zu berechnen und wir thematisieren diesen hier nicht näher.
Genaueres dazu findet sich z.B. auch in Fehlerarten auf Wikipedia.
Medizinische Tests können genauso als Tests verstanden werden. Ein klassischer HIV Test ist ein sogenannter ELISA (enzyme-linked immuno sorbent assay) Test. Dabei werden nicht die Viren direkt nachgewiesen sondern Antikörper nachgewiesen. Auch dieser Test hat eine Entscheidungsregel (analog: «mehr als 8 Tassen») und eine Wahrheit (analog: «p=0.5» oder nicht).
Für den ELISA-HIV Test sind die Fehlerwahrscheinlichkeiten der 1. und 2. Art bekannt (als populärwissenschaftliche Quelle z.B. diese Webseite):
| Modellwelt (Tatsächlicher Gesundheitszustand) | |||
|---|---|---|---|
| Ja | Nein | ||
| Beob. Welt (Diagnose) | Ja | 99.3% | 0.7% |
| Nein | 0.03% | 99.97% | |
Man sagt der Fehlerwahrscheinlichkeiten der 1. Art auch «true-positive rate» oder «Sensitivität», der Fehlerwahrscheinlichkeiten der 2. Art auch «true-negative rate» oder «Spezifizität».
Eine wichtige grösse für Testproblem ist auch die sogenannte «baserate» oder «Prävalenz»: Diese gibt an, wie viel Personen einer Grundgesamtheit an einer fraglichen Erkrankung leiden: In Europa beträgt die Prävalenz von HIV ca. $0.2\%$ in Schwarzafrika z.T. bis zu $5\%$.
Vierfeldertafel
Gehe für eine Vierfeldertafel beim Elisatest von einer Tabelle wie oben aus. Die vier Felder sind «Hat HIV:Test positiv», «Hat HIV:Test negativ», «Hat kein HIV:Test positiv», «Hat kein HIV:Test negativ». Gehe von einer Gesamtpopulation von $10000$ Personen aus und befülle die entsprechenden Felder. Achtung: Man kennt die Spaltentotale. Auf Grund der Spaltentotale kann man dann die Personen in den einzelnen Zellen auf Grund der Fehlerwahrscheinlichkeiten der 1. und 2. Art berechnen. Zählt man nacher die Spalten zusammen, kann man neue Schlüsse ziehen.
Fertige zu diesem Zweck eine Excel-Tabelle an und wähle die Fehlerraten und die Prävalenz als Steuerzellen.
$t$-Test
Grundsätzlich ist auch die Testfrage «Unterscheiden sich zwei Mittelwerte?» denkbar. Zu diesem Zweck wird angenommen, dass «$H_0$: Sie unterscheiden sich nicht» ist. Unter dieser Annahme («Modellwelt») kann nun wieder Fehler 1. und 2. Art berechnet werden, wenn man davon ausgeht, dass die zugrunde liegenden Daten normalverteilt sind.
In Excel wie in R kann dieser Test durchgeführt werden. Die Ausgabe dieses Tests, ist das kleinste möglich Niveau, zu dem $H_0$ gerade noch verworfen wird. Der erhalten Wert heisst auch $p$-Wert. Liegt nun dieser $p$-Wert unterhalb des vorgegeben Signifikanzniveaus von $5\%$, sagt man, dass sich die Mittelwert signifikant unterscheiden.
Lektion 13
Ziele
- Jede/r kann einen $t$-Test rechnen
- Jede/r hat für sich ein Mini-Projekt gewählt, welches er/sie über die nächsten beiden Male bearbeitet.
Auträge
- Feedbackbogen ausfüllen
- Theorie unten durcharbeiten
-
- Erstelle ein Histogramm für die vier Fälle
- Berechne jeweils den Mittelwert und die Varianz für die vier Fälle
- Führ einen $t$-Test durch um die Mittelwerte in beiden Fällen zu vergleichen. Wie gross ist der $p$-Wert?
- Unterscheidet sich der Preis von schwarz-metallisierten (schwarz mt) und weissen X5er BMWs signifikant?
- Projekt auswählen / kreieren
Mögliche Projektfragen
- Welche Farbe hat den höchsten Wiederverkaufswert?
- Bei welchem Modell ist der Zusammenhang zwischen gefahrenen Kilometern und Preis am stärksten?
- Welches ist die beliebeste Farbe? Ist die Modellabhängig?
- Kann von Hubraum auf die Energieeffizient geschlossen werden?
- Haben geschaltete Autos einen tieferen/höheren Verbrauch als Automatik Autos? Bei allen Modellen?
- Bestimme ein einfaches Modell um den Preis eines beliebigen Occassionsauto zu bestimmen.
Theorie
Bei der «tea tasting lady» war die Fragestellung, ob sie in Tat und Wahrheit bennenen konnte, ob denn nun die Milch vor dem Tee in der Tasse war oder umgekehrt. Statistisch hat sich das wie folgt formulieren lassen
- $H_0$: $p=0.5$ (heisst: die Lady kann es nicht, ihr Erfolg ist zufällig)
- $H_A$: $p>0.5$ (heisst: die Lady kann es nicht zufällig)
Man sagt $H_0$ auch Nullhypothese; $H_A$ ist dann die Alternative. Beschränkt man nun den Fehler erster Art (z.B. auf 5%) und sucht sich die entsprechende Anzahl Tassen, die richtig erkennt werden müssen hat man einen Test geschaffen, der überprüft zu, ob die Lady es zufällig kann.
Häufig funktionieren Tests aber auch umgekehrt: Das heisst, man formuliert die Nullhypothese ($p=0.5$) und übergibt die Anzahl der richtig erkannten Tassen. Als Resultat (von Hand für uns noch unmöglich; aus Excel oder R) erhält man dann, die Irrtumswahrscheinlichkeit oder den $p$-Wert. Das ist die Wahrscheinlichkeit, mit welcher eben ein Fehler erster Art begangen wird. Die Nullhypothese wird verworfen, wenn der $p$-Wert kleiner als ein bestimmtes Signifikanzniveau ist (z.B. $p$-Wert kleiner als 5%).
Das Problem der «tea tasting lady» ist nur ein stellvertretendes Problem für die statistische Testproblematik. Man stelle sich vor, man möchte die kognitive Leistung (gemessen in IQ Punkten in einem Test) zweier Gruppen vergleichen. Die eine Gruppe erhält ein koffeinhaltiges Getränke, die andere Gruppe nur ein Getränk ohne Koffein.
Die Frage ist nun offesnichtlich, ob die mittleren IQ-Werte der beiden Gruppen ($\mu_1$ und $\mu_2$) identisch oder verschieden sind.
Klar ist, dass man diese Mittelwerte einfach berechnen könnte, diese vergleichen und dann schliessen, dass die eine Gruppe besser ist als die andere. Das Problem dabei ist aber, dass die erbobenen IQ-Werte auch einer gewissen Schankung unterliegen, resp. Zufall beinhalten. Das heisst, es könnte sein, dass ein Unterschied in den Mittelwerten beobachtet wird, dieser aber rein zufällig zu Stande gekommen ist und nicht «struktureller» Natur ist. Zufällige Unterschiede sind aber nicht von Interesse.
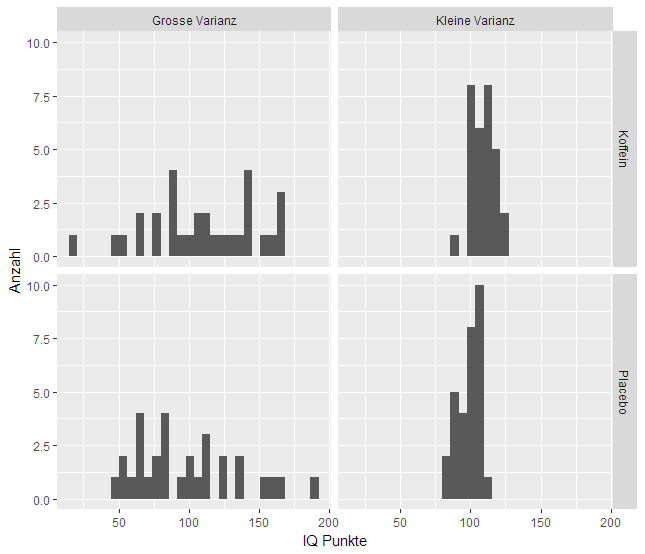 In der Graphik oben sind zwei Situation illustriert: Beide haben Verteilungen haben den gleichen Mittelwert von IQ-Punkten in der “Koffein” resp. “Placebo” Gruppe. Die Wahrscheinlichkeit, dass Resultat in der linken Spalte zufällig zu Stande gekommen ist, scheint aber ungleich grösser.
In der Graphik oben sind zwei Situation illustriert: Beide haben Verteilungen haben den gleichen Mittelwert von IQ-Punkten in der “Koffein” resp. “Placebo” Gruppe. Die Wahrscheinlichkeit, dass Resultat in der linken Spalte zufällig zu Stande gekommen ist, scheint aber ungleich grösser.
Das heisst, man formuliert also die Hypothesen $H_0:\mu_1=\mu_2$ und $H_A:\mu_1\neq \mu_2$. Analog zur «tea tasting lady» geht man davon aus, dass kein Unterschied besteht und versucht einen Test dafür zu schaffen.
Diese Idee wird nun durch den $t$-Test formalisiert: Dieser testet (unter gewissen Annahmen), ob ein Unterschied zufällig ist oder nicht. Berichtet wird dann ein $p$-Wert. Ist dieser denn kleiner als das vorgegeben Signifikanziveau, kann man die Nullhypothese von gleichen Mittelwerten ($\mu_1=\mu_2$) verwerfen und es liegt ein Unterschied vor.
Die zentrale Annahme des $t$-Tests ist, dass die beiden zu vergleichenden Grössen normalverteilt sind. Weiter gibt es noch folgende Annahmen, die man spezifieren muss:
- Gepaarter Test: Die beiden Beobachtungen in den Gruppen stammen vom gleichen Subjekt (vorher/nachher Tests)
- Homogene Varianzen: Die Varianz in beiden Gruppen ist gleich gross.
Beide Annahmen müssen spezifiert werden, da die Berechnung anders ausfällt.
- Excel:
=T.TEST(daten1;daten2;typ)dertypist $1$ für gepaart, $2$ für gleiche Varianzen, $3$ für ungleiche Varianzen - R:
t.test(daten1,daten2,paired=TRUE|FALSE,var.equal=TRUE|FALSE)wobeipairedeben für gepaarte Stichproben steht undvar.equalfür gleiche Varianzen.
Begriffe
Begriffe, die festzuhalten sind:
| Begriff | Kurzbeschrieb | Excel | R |
|---|---|---|---|
| Mittelwert | Arithmetisches Mittel ($\mu$). Man schreibt auch $\bar x$. | MITTELWERT() | mean() |
| Anzahl | Anzahl | ANZAHL() | length() |
| Merkmal | Eigenschaften eines Datenpunkts (z.B. Türen, Farbe etc.) | ||
| Merkmalsausprägung - und typen | Nominal (Farbe), Ordinal (Modell: X1 bis X6), Kardinal (z.B. Kilometer, Preis) | ||
| Datenblatt | |||
| Pivot-Tabelle | |||
| Filtern | |||
| Absolute und relative Häufigkeit von $x$ | Die absolute Häufigkeit entsprichen dem insgesamten Vorkommen, die relative Häufigkeit ist das Vorkommen in Prozent, d.h., die absolute Anzahl dividiert durch die Gesamtanzahl | ANZAHL() oder SUMMEWENN() | |
| Histogramm | Illustration von Daten. Die Säulenfläche ist proportional zur relativen Häufigkeit | ||
| Varianz | Die mittlere quadratische Abweichung, i.e. $\sigma^2=\frac1{n-1}\sum_{i=1}^n (x_i-\bar x)^2$ | VARIANZA() | var() |
| Standardabweichung | Wurzel der mittleren quadratischen Abweichung $\sigma=\sqrt{\frac1{n-1}\sum_{i=1}^n (x_i-\bar x)^2}$ | STABWA() | sd() |
| Median | Wert der mittig in der Verteilung aller sortierten Werte ist, resp. zum 50% Prozentrang gehöriger Wert | MEDIAN() | median() |
| Signifikanz | Prozentzahl welche den Fehler erster Art (eines Tests) beschränkt. | ||
| Test | Eine statistische Entscheidungsregel, welche überprüft, ob ein Resultat zufällig ist oder nicht. | ||
| Nullhypothese | Eine Hypothese, die überprüft wird und ggf. zu Gunsten der Alternativhypothese verworfen wird. | ||
| Alternativhypothese | Eine Hypothese, die zutrifft, wenn die Nullhypothese nicht zutrifft. | ||
| $p$-Wert | Auch Überschreitungswahrscheinlichkeit oder Signifikanzwert. Wahrscheinlichkeit mit derer ein Fehler erster Art begangen wird. | ||
| $\alpha$-Quantil | Zum Prozentrang $\alpha$ gehöriger Wert | QUANTIL.INKL() | quantile(,,type=2) |
| Modus | Der häufigste (die häufigsten) Wert(e) | MODUS.EINF() |
|
| IQA | Interquartilsabstand. Differenz des 1. und 3. Quartils | ||
| Boxplot | Illustration der Verteilung mit Quartilen | boxplot() |
|
| Outlier | Ausreisser. Eine mögliche Definition für Outlier, sind Werte, die ausserhalb der Whiskers beim Boxplot sind | ||
| Lorenzkurve | Mass zur Konzentration einer Verteilung. Es wir dabei die relative kumulierte Anzahl gegen die relative kumulierte Summe des Merkmals gezeichnet | ||
| Gini-Koeffizient | Mass der Konzentration einer Verteilung welches die Fläche misst, welche die Lorenzkurve mit der Winkelhalbierenden einschliesst | ||
| Normalverteilung | Auch Gaussverteilung. Häufige Verteilung von Merkmalen. Das Histogamm gleich dabei einer Glockenkurve | ||
| Standardisieren | Zentrierung und Streckung eines Merkmals zu $Z=\frac{X-\mu}{\sigma}$. Es ist dann $\mu_Z=0$ und $\sigma_Z=1$ | ||
| Korrelation | Mass für einen linearen Zusammenhang zwischen $-1$ und $1$ | KORREL() | cor() |
| Scatterplot | Graphische Darstellung zweier Merkmale als $x$ und $y$-Koordinate | Einfügen $xy$… | plot(x,y) |
| Bestimmtheismass | Quadrat der Korrelation, zur Messung der Stärke eines Zusammenhangs | ||
| Erklärende Variable | Variable (z.B. Kilometer) welche die abhängige Variable (z.B. Preis) in einer Regression erklären soll | ||
| Regression | Bestimmung einer linearen Funktion, welche den Zusammenhang zwischen erklärender und abhängier Variable herstellt | ||
| Koeffizienten | Abschnitt und Steigung der linearen Funktion einer Regression | ||
| Dummy-Variabel | Variable mit den Ausprägungen $0$ und $1$ um eine nominale Variable in einer Regression zu verwenden | ||