Buildingblocks für Animationen

Eine Gleichmässige Bewegung (linear oder rotierend) kann durch eine lineare Funktion in der Zeit (in POV-Ray clock) beschrieben werden.

Gegeben sind zwei Punkte $A$ und $B$. Sei $\vec v = \overrightarrow{AB}$.

Die Punkte $P$ zwischen $A$ und $B$ können für Zeiten $t \in [0,1]$ wie folgt beschrieben werden: $$ \overrightarrow{OP}(t) = \overrightarrow{OA} + t \cdot \vec v = \overrightarrow{OA} + t \cdot \left(\overrightarrow{OB}-\overrightarrow{OA}\right) $$

Überprüfen Sie durch einsetzen, dass für $t=0$ und $t=1$ auch tatsächlich die gewünschten Koordinaten geliefert werden.

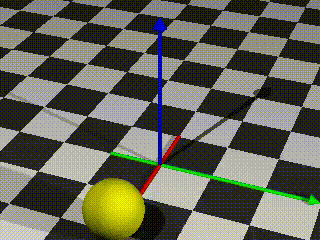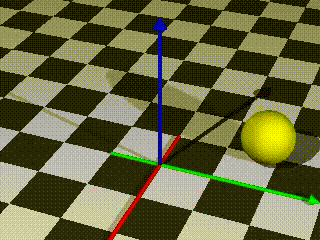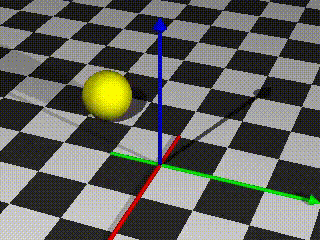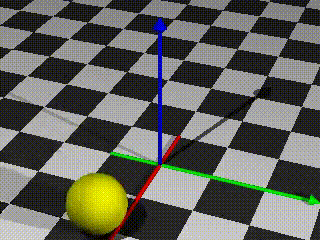
#declare start = <-2,-3,1.5>;
#declare ende = <1,2,0.5>;
 
// Lineare Bewegung vom Punkt 'start' zum Punkt 'ende':
// Sei 'vektor' der vektor von start zu ende, also vektor = ende-start
// Position = start + clock*vektor
 
sphere {
	start + clock*(ende-start), 0.3  // Kugel mit linearer Bewegung von start zu ende
	pigment {color rgb x+y}
}

Wenn in der Zeit $t$ von 0 bis 1 eine volle Umdrehung gemacht werden soll, muss der Drehwinkel $\alpha$ von $0^\circ$ bis $360^\circ$ variieren. Wenn dies gleichmässig erfolgen soll erhält man folgende lineare Funktion für den Winkel: $$ \alpha(t) = 360^\circ \cdot t $$

// Gleichmässige Rotation:
// Zum Zeitpunkt 0 ist der Winkel 0, zum Zeitpunkt 1, 360 also
// winkel = 360*clock
 
sphere {
	<2,0,0.5>, 0.5
	rotate 360*clock*z
	pigment {color rgb x+y}
}

Eine gleichmässig beschleunigte Bewegung wird durch eine quadratische Funktion beschrieben, mit quadratischem Koeffizienten $\frac{1}{2}a$, wobei $a$ die Beschleunigung ist.

Meistens werden aber einfach die Nullstellen der Parabel und die Höhe des Scheitels gewählt, damit die Animation passt.

Wir betrachten einen Wurf (oder Fall) der zur Zeit 0 am Boden nach oben startet und zur Zeit 1 wieder am Boden ankommt. Dabei soll die Höhe $h$ erreicht werden.

Gesucht ist damit eine quadratische Funktion mit

Nullstellen 0 und 1
Scheitelpunkt $(0.5, h)$. (Der Scheitelpunkt liegt genau zwischen den Nullstellen).

Folgende Funktionen haben die Nullstellen 0 und 1: $f(x) = a \cdot x\cdot(1-x)$, mit $a \in \mathbb{R}^\star$.

Wir möchten dass $f(0.5)=h$, was uns eine Gleichung für $a$ liefert: $a\cdot 0.25 = h$, also $a=4h$.

Die gesuchte $z$-Koordinate ist also: $$ z(t) = 4h\cdot t \cdot (1-t) $$

Überprüfen Sie durch Einsetzen, dass zu den Zeitpunkten $t \in \{0,0.5,1\}$ die gewünschten Höhen erreicht werden.

Skizzieren Sie den Funktionsgraphen für $h=1$.

#declare hoehe=2;
 
// Gleichmässig beschleunigte Bewegung vom Ursprung auf die Höhe 2 und zurück.
// Die Höhe ist eine Quadratische Funktion mit f(0)=0, f(1)=0 und f(0.5)=hoehe.
// Da die Nullstellen bekannt sind, kann die Funktion als f(x)=a*x*(1-x) mit
// noch zu bestimmenden Öffnungsfaktor a geschrieben werden. Damit ist schon einmal
// f(0)=f(1)=0 gegeben. Durch einsetzen erhält man f(0.5)=0.25*a. D.h. a muss also
// als 4*hoehe gewählt werden.
sphere {
	4*hoehe*clock*(1-clock)*z, 0.3  // Kugel mit z-Koordinate als quadratische Funktion mit Nullstellen zur Zeit 0 und 1, gegebene Scheitelhöhe.
	pigment {color rgb x+y}
	translate 0.3*z  // Damit die Kugel den Boden berührt und nicht darin versinkt.
}

Eine lineare Bewegung in $x/y$-Richtung und eine quadratische in $z$-Richtung werden kombiniert (siehe oben für die Details zu den einzelnen Bewegungen): $$ $$

#include "markierungen.inc"
 
#declare hoehe=2;
// Start und Ende auf selber Höhe!
#declare start=<0,-2,0>;
#declare ende=<0,2,0>;
 
// die Bewegung parallel zur x-y-Ebene erfolgt linear,
// die Bewegung in z-Richtung ist quadratisch
sphere {
	start+clock*(ende-start) + 4*hoehe*clock*(1-clock)*z, 0.3  // Kugel mit linearer Bewegung von start zu ende, plus quadratische z-Koordinate
	pigment {color rgb x+y}
	translate 0.3*z  // Damit die Kugel den Boden berührt und nicht darin versinkt.
}

Schwingungen können durch eine Sinus-Funktion beschrieben werden, die gestreckt und verschoben wird. Folgende Parameter bestimmen eine Schwingung:

Amplitude $a$ (die Hälfte der Differenz des kleinsten und grössten Werts)
Periode $p$ (Dauer einer Schwingung)
Phase $\phi$ (Winkel zur Zeit Null)
Mittelwert $m$ (Durchschnitt des kleinsten und grössten Werts)

Der Funktionsterm lautet (Winkelangaben in Radianten!) $$ f(t) = a \cdot \sin\left(\phi + t\cdot 2\pi \cdot p\right) + m $$

Bestimmen Sie obige Parameter für eine Schwingung, die in einer Zeiteinheit eine Schwingung zwischen den Werten 0 und 1 ausführt. Für die Phase kann $\phi=0$ gewählt werden.

#declare start = <-2,-3,1.5>;
#declare ende = <1,2,0.5>;
 
// Lineare Schwingung vom Punkt 'start' zum Punkt 'ende':
// Sei 'vektor' der vektor von start zu ende, also vektor = ende-start
//
// Wir brauchen eine Schwingung, die in der Zeit 1 eine volle Schwingung zwischen
// den Positionen 0 und 1 vollführt.
// f(t) = 0.5*sin(t*2*pi)+0.5
//
// Diese Funktion beschreibt die Position zwischen dem Start- und Endpunkt
// Position = start + f(clock)*vektor
 
sphere {
	start + (0.5*sin(clock*pi*2)+0.5)*(ende-start), 0.3  // Kugel mit linearer Bewegung von start zu ende
	pigment {color rgb x+y}
}

#declare auslenkung=20;  // Schwingung zwischen +/- auslenkung
// Wir brauchen eine Funktion, die zwischen -20 und +20 schwingt
// f(t) = sin(2*pi*t)*auslenkung
 
union { // Pendel mit Drehpunkt im Uhrsprung! Verschoben wird **nach** der Drehung
	sphere { 0, 0.1 }
	cylinder { 0, -2*z, 0.05 }
	sphere {-2*z, 0.3 }
	pigment {color rgb <1,1,0> }
	// Erst rotieren um die x-Achse:
	rotate auslenkung*sin(clock*2*pi)*x
	// Dann nach oben verschieben:
	translate 2.5*z
}

Idee: Wir teilen das Zeitintervall in Unterintervalle auf und berechnen jeweils eine neue Zeit von 0-1 in diesem Unterintervall:

#declare hoehe=2;
// Start und Ende auf selber Höhe!
#declare start=<0,-2,0>;
#declare ende=<0,2,0>;
 
sphere{
	<0,0,0.3>, 0.3
	pigment { color rgb <1,1,0> }
 
	// Zwei Bewegungen, je nach clock:
	#if (clock<0.5)
		#declare myclock = clock*2;  // Wieder Werte von 0 bis 1
		translate 2*y
		rotate -180*myclock*z
	#else
		#declare myclock = (clock-0.5)*2; // Wieder Werte von 0 bis 1
		translate (4*myclock-2)*y    // Linear in y-Richtung
		translate 4*3*(1-myclock)*myclock*z   // Quadratisch in z-Richtung (bis auf Höhe 3)
	#end
}

POV-Ray hat kein else if, dafür ein praktische switch, range statements.

Mit dem switch statement wird ein Wert untersucht. Mit range(a,b) wird überprüft, ob der Wert im (leider beidseitg geschlossenen) Intervall $[a,b]$ liegt.

torus {1, 0.3
	pigment {checker color rgb x, color rgb z}
	finish { phong 0.7 reflection 0.1 }
	rotate 90*x
	translate x-y
 
	#switch (clock)
		#range (0, 0.2499)
			#declare myclock = 4*clock;
			rotate -180*x*myclock
			#break  // Ende von diesem range-block (sonst wird der nächste automatisch auch ausgeführt)
		#range (0.25, 0.4999)
			#declare myclock = 4*(clock-0.25);
			rotate -180*x
			rotate -180*y*myclock
			#break
		#range (0.5, 0.7499)
			#declare myclock = 4*(clock-0.5);
			rotate -180*x
			rotate -180*y
			rotate 180*x*myclock
			#break
		#range (0.75, 1)
			#declare myclock = 4*(clock-0.75);
			rotate -180*x
			rotate -180*y
			rotate 180*x
			rotate 180*y*myclock
			#break
	#end  // ende vom switch
	translate 0.3*z // Damit der Torus nicht im Boden liegt
}

Anstatt myclock für jeden Fall neu zu berechnen, könnte hier auch myclock vor dem switch wie folgt definiert werden

#declare myclock = 4*clock - floor(4*clock)   // floor rundet auf die nächste Ganzzahl ab

oder etwas eleganter

#declare myclock = mod(4*clock, 1)   // Rest der Ganzzahldivision von 4*clock geteilt durch 1

Die vier Definitionen in den #range Abschnitten können so gelöscht werden.

Die Animation kann noch ansprechender gemacht werden, wenn die Drehung nicht gleichmässig ist, sondern am Anfang und Ende schneller und dazwischen langsamer (als ob der Torus fallen würde). Das kann entweder physikalisch korrekt gerechnet werden (was nicht ganz ohne ist) oder angenähert werden.

Gehen Sie dazu wie folgt vor:

Skizzieren Sie auf Papier die Funktion $f(t) = t$, was dem linearen Drehwinkel entspricht.
Skizzieren Sie ins gleiche Koordinatensystem die gewünschte Funktion $g(t)$, die am Anfang bei $g(t)=0$ steiler ansteigt, bei $t=0.5$ ebenfalls den Wert 0.5 liefert (aber weniger steil ist) und bei $g(1)=1$ ebenfalls steiler ist.
Skizzieren Sie die Differenz $d(t) = g(t)-f(t)$ und bestimmen Sie eine Funktion, die in etwa die Form von $d(t)$ hat.
Unsere gesuchte Funktion ist also $g(t) = f(t)+d(t) = t+d(t)$.
Fügen Sie dann in POV-Ray eine Zeile nach der Definition der Variablen myclock ein:

#declare myclock = myclock + //hier Ihre Funktion d einfügen

Jetzt sollte die Bewegung natürlicher wirken.

Mit «natürlicherer» Bewegung (aber immer noch physikalisch inkorrekt):

Noch eleganterer Code für diesen Fall

Betrachten wir die Funktion für den Drehwinkel der z.B. zweiten Drehung, kann die Funktion wie folgt beschrieben werden:

$$ f(t) = \left\{\begin{array}{ll} 0^\circ & \text{wenn }t<0.25 \\ 180^\circ & \text{wenn }t>0.5 \\ 180^\circ \cdot (t-0.25)*4 & \text{sonst} \end{array} \right. $$

POV-Ray bietet eine Funktion clip(v,min,max), die v liefert, wenn v zwischen den Werten min und max. Wenn v kleiner als min ist, liefert die Funktion den Wert min, wenn v grösser als max ist, liefert die Funktion den Wert max. Damit kann obiger Code gänzlich ohne if geschrieben werden:

// Einfachere Formeln, wenn clock gleich schon mit 4 multipliziert wird
#declare myclock=4*clock;
//
// ... 
// 
 
    rotate clip(myclock,   0, 1)*-180*x   // Erste Rotation (Startet sofort, stoppt nach myclock=1)
    rotate clip(myclock-1, 0, 1)*-180*y   // Zweite Rotation (Startet erst bei myclock=1, stoppt nach myclock=2)
    rotate clip(myclock-2, 0, 1)*180*x    // Dritte Rotation
    rotate clip(myclock-3, 0, 1)*180*y    // Vierte Rotation