Adventsstern aus einem Quadrat, nur falten und einscheiden (ergibt den Winkel $\alpha=22.5^\circ$, siehe unten). Der daraus enstehende Stern ist unten nicht flach.

Die Frage ist, wie muss das Schnittmuster sein, damit ein unten flacher Stern entsteht (damit man diese z.B. zusammenkleben oder auf ein Fenster kleben kann).

Wir führen folgende (ziemlich beliebige) Notation ein:

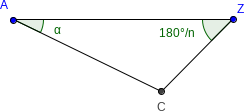
• $Z$ ist das Zentrum vom Stern
• $A$ ist ein Punkt auf einer Zacke vom Stern
• $C$ ist der Punkt, bis wohin eingeschnitten wird.
• Der Winkel $\alpha$ kann gewählt werden.
• $n$ sind die Anzahl Zacken des Sterns.
• Der Winkel im Zentrum ist $\frac{180^\circ}{n}$, weil der Stern rotationssymmetrisch sein soll.

Die Frage ist, was passiert mit der Figur im 3-dimensionalen Raum, wenn der Stern gefaltet wird. Folgende Einsichten sind wichtig:

• Von oben betrachtet, erscheinen die Winkel bei Z immer gleich gross.
• Wir wollen einen unten flachen Stern. Darum ist es vorteilhaft, beim Auffalten des Stern die Strecke $AC$ zu fixieren und den Rest des Sterns um diese Achse zu drehen.
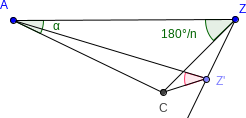
• Betrachtet man die Drehung um $AC$ von oben, bleiben $A$ und $C$ liegen, und $Z$ bewegt sich auf der Senkrechten zu $AC$ durch $Z$.
• Wir suchen $Z'$ also so, dass der Winkel $AZ'C$ wieder $\frac{180^\circ}{n}$ ist.

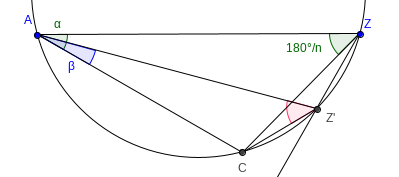
• D.h. $Z'$ liegt auf dem Ortsbogen, der einfach dem Umkreis von $AZC$ entspricht (darin sind die Winkel bei $Z$ und $Z'$ dann Peripheriewinkel über der Sehne $AC$).

• Das Dreieck $AZ'C$ entspricht der Ansicht von oben einer halben Zacke des gefalteten Sterns. Damit sieht man auch den halben «Zackenwinkel» $\beta$.
• Der Teil vom Papier, der unten am Stern umgefaltet wird, muss also den Winkel $2\beta$ zur Strecke $AC$ bilden, damit der Stern möglichst einfach geklebt werden kann.
• Der Winkel $\alpha$ muss natürlich so gewählt werden, dass die Senkrechte den Ortsbogen in der Skizze unterhalb von $AZ$ schneidet (grösser kann das Dreieck beim Drehen nicht werden).

Sie finden hier eine Anleitung, um die Parameter beliebiger Sternvorlagen (d.h. beliebige Winkel $\alpha$ und Anzahl Zacken $n$) in GeoGebra zu konstruieren.

Konstruiert wurde mit GeoGebra online: https://www.geogebra.org/geometry

Hier geht's zum ScreenCast oder Screencast auf SharePoint

Und die fertige GeoGebra-Konstruktion.

• Auffalten mit GeoGebra 3D: https://www.geogebra.org/calculator/vff75kwe

Folgendes Python-Programm erzeugt SVG-Dateien mit Schnittmustern.

stern.py

Die gewünschte Anzahl Zacken und der Winkel $\alpha$ werden am Anfang des Programms direkt im Code festgelegt (Zusatzaufgabe: Programm so erweitern, dass die Parameter direkt auf der Kommandozeile angegeben werden können.

Mit Inkscape können SVG-Dateien erstellt und bearbeitet werden. Konversionen zwischen Datei-Formaten können auch auf der Kommandozeile stattfinden, z.B. mit

inkscape -o output.pdf input.svg

Um einen ganzen Haufen Dateien zu konvertieren kann z.B. wie folgt vorgegangen werden:

for svg in n*svg
do
  echo Konvertiere $svg
  pdf="$svg".pdf
  inkscape -o "$pdf" "$svg"
done

Das liefert dann einzelne pdf-Dateien. Alternativ können die SVG-Dateien natürlich auch in Inkscape erst noch bearbeitet werden (z.B. Grösse und Position ändern.

schnittvorlagen.pdf