Tabellenkalkulationsaufgaben

Alle Tabellenkalkulationsfunktionen sind hier im englischen Syntax aufgeführt und funktionieren genau so im englischen OpenOffice. Die Übersetzung in die deutsche Excel-Version wird angegeben, wo möglich.

Im Deutschen werden Funktions-Argumente durch Strichpunkte anstatt Kommas getrennt. Dezimalzahlen werden im Deutschen mit Kommas anstatt Punkten geschrieben. Die englischen Funktionsnamen sind universell und in den meisten Programmiersprachen und Anwendung gleich oder sehr ähnlich. Die deutschen Übersetzungen sind - gewöhnungsbedürftig.

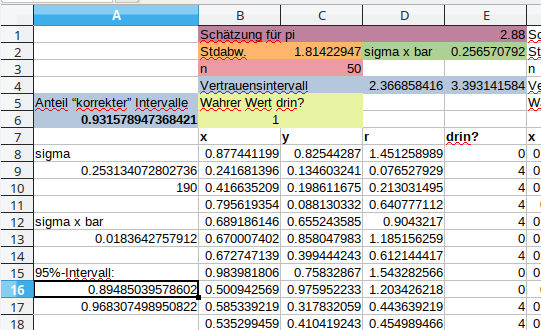
Sie haben letztes Mal $\pi$ durch ein Zufallsexperiment bestimmt. Es geht in dieser Übung darum, zusätzlich noch ein 95%-Vertrauensintervall für die Messung zu bestimmen. Dazu sind noch ein paar Anpassungen nötig:

1. Fügen Sie genügend leere Zeilen vor der Messung ein.
2. Die gesamte Messung muss auf 4 Spalten Platz haben (damit diese kopiert werden können, um das Experiment zu wiederholen).
3. Ändern Sie das Resultat des Experiments von 0 oder 1 zu 0 oder 4. Damit ist die Schätzung direkt der Mittelwert aller Messwerte. Passen Sie das entsprechend an.
4. Berechnen Sie die Standardabweichung der Messwerte mittels STDEV.S(bereich), bzw. STABW.S(bereich). Das 'S' steht für “Sample” und wird in fast allen Fällen eingesetzt.
5. Berechnen Sie die Anzahl Messwerte $n$ mit der Funktion COUNTIF(bereich,“<>”), bzw. ZÄHLENWENN(bereich;“<>”). Wählen Sie den Bereich ruhig viel grösser. Damit können Sie später die Anzahl Versuche erhöhen.
6. Berechnen Sie nun die Standardabweichung des Mittelwerts aus der Standardabweichung der Messwerte und dereren Anzahl. Man erhält diese durch Division durch $\sqrt{n}$. Funktion SQRT(), bzw. WURZEL().
7. Berechnen Sie daraus ein 95%-Vertrauensintervall $[\mu - 2\sigma_{\mu}, \mu + 2\sigma_{\mu}]$.
8. Bestimmen Sie, ob $\pi$ im Vertrauensintervall liegt (1), oder nicht (0). Verwenden Sie dazu sie Funktionen IF(bedingung,1,0), PI() und AND(bedingung1, bedingung2), bzw. auf Deutsch: WENN und UND. Dieses Resultat soll alleine auf einer Zeile stehen.
9. Berechnen Sie das Tabellenblatt mehrmals neu mit F9. In ca. 1 von 20 Fällen sollte $\pi$ nicht im Vertrauensintervall liegen.
10. Kopieren Sie dann die vier Spalten ca. 200 mal nach rechts.
11. Berechnen Sie den Durchschnitt der 1/0-Werte, ob das Vertrauensintervall $\pi$ enthalten hat. Man erwartet Werte um die 95% für den Anteil “korrekter” Intervalle.
12. Spielen Sie mit F9. Was stellen Sie fest? Was ist Ihre Vermutung?
13. Erstellen Sie ein Vertauensintervall für den “Anteil korrekter Intervalle”. Feststellung?
14. Erhöhen Sie die Anzahl Versuche pro Experiment auf 200. Wie sieht es jetzt aus?

Machen Sie sich erst eine Skizze auf Papier, bevor Sie die Sache in einem Tabellenkalkulationsprogramm umsetzen.

Im 2-dimensionalen Koordinatensystem betrachtet man das achsenparallele Quadrat mit Eckpunkten $(0,0)$ und $(1,1)$, sowie den darin einbeschriebenen Viertel des Einheitskreises.

1. Berechnen Sie den Inhalt folgender Flächen:
   • Viertel vom Einheitskreis: $A_k$
   • Quadrat $A_q$.
2. Wenn man zufällig einen Punkt im Quadrat auswählt, wie gross ist die Wahrscheinlichkeit, dass der Punkt auch noch im Kreis liegt?
3. Die Excel-Funktion RAND() (bzw. ZUFALLSZAHL() auf deutsch) liefert eine “reelle” Zahl zwischen 0 (inklusive) und 1 (exklusive). Erzeugen Sie damit die Koordinaten eines zufälligen Punktes im Quadrat.
4. Wie kann man mathematisch bestimmen, ob ein Punkt mit gegeben Koordinaten im Einheitskreis liegt oder nicht?
5. Mit der Excel-Funktion IF(bedingung, Wert wenn wahr, Wert wenn falsch) (bzw. WENN(…) auf deutsch) kann der Inhalt der Zelle in Abhängigkeit eine Bedingung gesetzt werden. Z.B. mit =IF(A3<1, 1 , 0) wird die Zelle 1, wenn der Inhalt der Zelle A3 kleiner als 1 ist, sonst wird der Inhalt 0.
6. Arrangieren Sie Ihr Tabellenblatt wie folgt:
7. Bestimmen Sie 50 Punkte in der gleichen Kolonne.
8. Berechnen Sie den Durchschnitt AVERAGE(bereich)) (bzw. MITTELWERT(bereich)) aller 0/1-Werte. Wie gross müsste dieser theoretisch sein, wenn man extrem viele Punkte zufällig wählt?
9. Berechnen Sie aus dem Durchschnitt eine Schätzung für $\pi$.
10. Berechnen Sie die prozentuale Abweichung der Schätzung von $\pi$. Drücken Sie mehrmals F9, um das Experiment mit neuen Zufallszahlen zu wiederholen. Take home message: Mit so grossen Fehlern müssen Sie rechnen, wenn Sie bei einer Umfrage 50 Leute befragen!.

Ziel ist es, viele Male (>100) folgendes Experiment zu wiederholen: Eine Münze wird 50 mal geworfen. Das Resultat eines Experiments ist wie viel mal “Zahl” geworfen wurde.

Von den vielen Experimenten wird ein Häufigkeitsdiagramm gezeichnet.

Zusatz: Bestimmen Sie experimentell, in wie vielen Prozent der Experimente die Abweichung von 25 genau 0, höchstens 1, höchstens 2 etc. war.

Zur weiteren Analyse, hier die Resultate von gut 11 Millionen Experimenten:

[[0, 0], [1, 0], [2, 0], [3, 0], [4, 0], [5, 0], [6, 0], [7, 2], [8, 3], [9, 25], [10, 89], [11, 390], [12, 1203], [13, 3489], [14, 9225], [15, 22256], [16, 48835], [17, 97222], [18, 178848], [19, 299754], [20, 464974], [21, 664076], [22, 875155], [23, 1066766], [24, 1199690], [25, 1247248], [26, 1198924], [27, 1067217], [28, 875356], [29, 663539], [30, 464870], [31, 300087], [32, 178527], [33, 97105], [34, 48696], [35, 22186], [36, 9144], [37, 3463], [38, 1157], [39, 363], [40, 94], [41, 19], [42, 2], [43, 0], [44, 1], [45, 0], [46, 0], [47, 0], [48, 0], [49, 0], [50, 0]]

Wie kriegen Sie diese Daten am einfachsten in eine Tabellenkalkulation?

Die wichtigsten Funktionen:

• RANDBETWEEN(0,1) liefert eine Zufallszahl 0 oder 1 mit gleicher Wahrscheinlichkeit.
  • Deutsch: ZUFALLSBEREICH(0;1)
• SUM(bereich) liefert die Summe eines Bereichs, z.B. A1:A20.
  • Deutsch: SUMME(bereich)
• COUNTIF(bereich, bedingung) zählt die Anzahl Elemente im Bereich, die eine Bedingung erfüllen. Die Bedingung ist entweder eine Zahl (für Gleichheit) oder eine Zeichenkette beginnend mit einem Vergleichszeichen, wie z.B. = oder <. Z.B. COUNTIF(A1:A20, “<10”) zählt die Anzahl Zellen im Bereich A1:A20 die 1 enthalten.
  • Deutsch: ZÄHLENWENN(bereich;bedingung)
• Absolute Zellbezüge (d.h. die sich beim Kopieren nicht mitverschieben) können mit einem vorgestelltem \$-Zeichen eingeben werden, z.B. C\$4:K\$4 fixiert die Zeile 4.

Wird das Feld 28 häufiger besucht als die Nachbarfelder (weil Vielfaches von 7, durchschnittlicher Würfelwurf ist 3.5)

Häufigkeiten bei 10'000'000 Wiederholungen (Felder 1 bis 29)

[1666403, 1942816, 2269604, 2647553, 3085210, 3600863, 2537102, 2682600, 2804177, 2892126, 2933207, 2906309, 2793705, 2835480, 2860450, 2870657, 2866628, 2854988, 2849852, 2858039, 2858880, 2859729, 2856867, 2855446, 2854080, 2857855, 2858142, 2857399, 2859531]

Ruby Code

count = Array.new(28*6,0)
10000000.times{s=0; 28.times{count[s]+=1; s+=rand(6)+1}}
count[1..29]