Planimetrie, erster Teil
Experimentelle Mathematik mit GeoGebra (1rG am 25.11.2021; 1aLIM am 29.11.2021)
Installiere Geogebra von GeoGebra Classic 6 und starte das Programm.
Learning by doing: Mach dich mit GeoGebra vertraut, indem du die folgende Aufgabe bearbeitest.
Du wirst die Aufgabe nur dann lösen können, wenn du eigenständig das Programm erforschst (oder jemanden fragst oder im Internet suchst etc.): Spiele herum, erforsche die Menüpunkte/Icons, beginne die Zeichnung von neuem oder starte GeoGebra neu, wenn du dich verrannt hast oder zu viele Sachen falsch konstruiert hast. Mit Ctrl-Z bzw. einem Icon rechts oben kann du Konstruktionsschritte rückgängig machen.
Nur durch Herumspielen lernt man die Funktionen eines neuen Programms kennen!
Ausgezeichnete Punkte im Dreieck (USHI): Umkreismittelpunkt, Schwerpunkt, Höhenschnittpunkt, Innkreismittelpunkt
Teilaufgabe (a)
Bearbeite die Kurz- oder Langfassung.
Kurzfassung: Zeichne mit GeoGebra ein Dreieck und konstruiere seine vier ausgezeichneten Punkte $U$, $S$, $H$, $I$ samt Umkreis und Innkreis. Verbirg alle Objekte, die du nur zur Konstruktion benötigt hast. (Du bist dann noch nicht fertig: Unten wartet Teilaufgabe (b)!)
Langfassung:
- Zeichne mit GeoGebra drei Punkte $A$, $B$, $C$ und verbinde sie mit Strecken zu einem Dreieck. (Beachte: Der Mauszeiger verändert sich zu einer Hand, wenn ein Objekt auswählbar ist. Beim Verbinden von zwei Punkten sollte man den ersten Punkt anklicken und dann den zweiten. Man sollte nicht den ersten anklicken und die Maustaste gedrückt halten: Dann erscheint die Hand zum Auswählen des zweiten Punkts nicht.)
- U: Konstruiere den Umkreismittelpunkt (= Schnittpunkt der Mittelsenkrechten) des Dreiecks und ändere seinen Namen zu $U$ (rechte Maustaste). (Man kann den Schnittpunkt per Maus anklicken - sicherer ist es aber, die beiden zu schneidenden Objekte hintereinander anzuklicken, und zwar am besten weit draussen, wo sie eindeutig auswählbar sind.)
- Zeichne den Umkreis.
- Bewege mit dem “Bewege”-Werkzeug (der linke Icon in
) die Eckpunkte des Dreiecks und beobachte, wie sich der Umkreis ändert. - Optional: Wenn es dir gelingt: Verberge mit Hilfe der beiden Icons links in
ein eventuell vorhandenes Koordinatensystem bzw. quadratisches Raster (falls diese Icons nicht sichtbar sind: Klicke etwa auf das “Bewege”-Werkzeug). (In der klassischen Geometrie arbeitet man mit einem weissen Blatt Papier statt mit einem Karopapier (mit Koordinatensystem) - die alten Griechen zeichneten vermutlich im Sand.) - S: Konstruiere den Schwerpunkt (= Schnittpunkt der Verbindungen der Dreiecksecken mit den Mittelpunkten der gegenüberliegenden Seiten) und gib ihm den Namen $S$.
- Verberge der besseren Übersichtlichkeit halber alle Hilfslinien, die zur Konstruktion von $U$ und $S$ verwendet wurden (mit rechter Maustaste anklicken). (Alternativ kann man Objekte verbergen bzw. sichtbar machen durch Verwenden des Icons “Objekt anzeigen / ausblenden” ganz rechts in (vermutlich ist bei dir aktuell ganz rechts eine andere Wahl sichtbar; klicke darauf und wähle das Gewünschte). Dies hat auch den Vorteil, dass man verborgene Objekte wieder findet.)
- H: Konstruiere den Höhenschnittpunkt (= Schnittpunkt der Höhen) und gib ihm den Namen $H$.
- Verberge der besseren Übersichtlichkeit halber alle zur Konstruktion benötigten Objekte (Geraden, Punkte, Namen von Geraden etc.), so dass nur noch das Dreieck samt der Eckpunkte $A$, $B$, $C$, die Punkte $U$, $S$, $H$ und der Umkreis sichtbar sind.
- I: Konstruiere den Innkreismittelpunkt $I$ (= Schnittpunkt der Winkelhalbierenden).
- Vermutlich etwas schwieriger: Konstruiere den Inkreis so, dass er sich korrekt verändert, wenn du die Eckpunkte des Dreiecks bewegst.
- Verberge wieder die nur während der Konstruktion benötigten Objekte.
Melde, wenn ich wichtige Informationen vergessen habe oder du Fehler bemerkst!
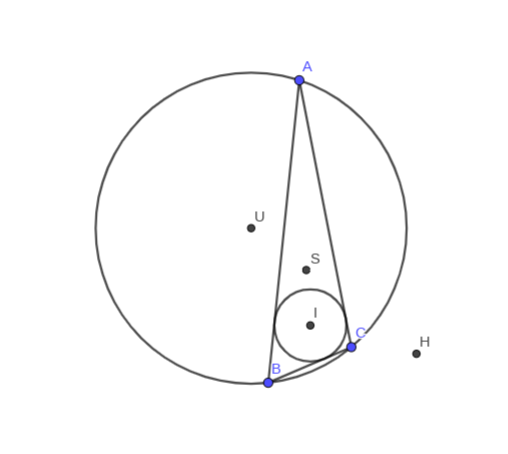
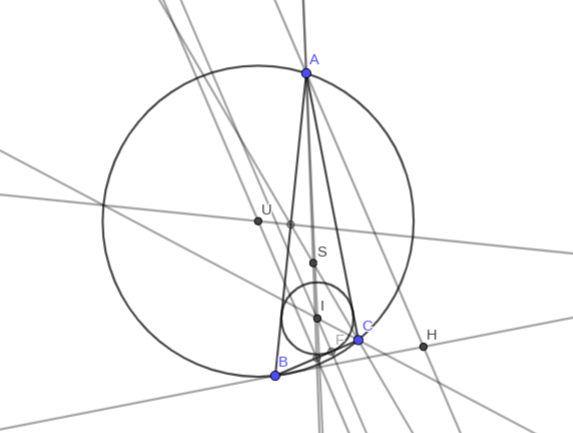
Deine Konstruktion sollte nun in etwa so aussehen:
Teilaufgabe (b)
Entdecke nun experimentell einen wichtigen allgemeinen Sachverhalt, der für alle Dreiecke gilt: Bewege die Eckpunkten des Dreiecks und beobachte, wie sich die vier ausgezeichneten Punkte $U$, $S$, $H$, $I$ des Dreicks verändern. Fällt dir etwas auf?
Zuerst spielen und nachdenken – nochmal nachdenken – und nochmal denken – viel später die Hinweise anschauen – wenn du selbst darauf kommst, wirst du es dir viel besser merken können!
GeoGebra versus Zeichnen mit Zirkel und Lineal
Beziehungsweise: Wie sollen wir in den Geometrie-Lektionen zeichnen?
Überlege, welche Vor- oder Nachteile GeoGebra gegenüber dem klassischen Konstruieren mit Zirkel und Lineal hat - zuerst, ohne die versteckten Listen anzuschauen.
Dann schau die Listen an und melde mir wichtige Punkte, die noch nicht vermerkt sind.
)Konstruktionsbeschreibungen befolgen und erstellen (1rG am 30.11. und 01.12.2021; 1aLIM am 30.11. und 01.12.2021)
Beim klassischen Konstruieren mit Zirkel und Lineal darf das Lineal (oder Geodreieck) nur zum Zeichnen von Geraden verwendet werden. Nicht verwenden darf man Massangaben auf Lineal oder Geodreieck: Man darf keine Strecken oder Winkel messen und keine parallelen oder senkrechten Geraden mit dem Geodreieck allein zeichnen. Auch die sonstigen Hilfslinien auf dem Geodreieck darf man nicht verwenden.
Ausgeteiltes Material (wird vermutlich bald durch das Gesamtskript samt Lösungen ersetzt):
planimetrie-grundlagen-sv-seiten-1-4.pdf
An die Leute zu Hause: Gute Besserung, falls nötig. Ich hoffe, ihr kommt klar und habt jemanden in der Klasse, der Euch bei Fragen hilft. Sonst kann ich auch Mal per Teams Fragen beantworten, es ist aber schwierig für mich, gleichzeitig in der Klasse individuell Fragen zu beantworten und per Teams präsent zu sein.
@1aLIM: Was du aus dieser To-do-Box nicht in der Lektion am Mittwoch schaffst, ist bis Montag individuell zu erledigen (Hausaufgabe).
Mathematisches
Bearbeite die Abschnitte 4.1 und 4.2 (also insbesondere die Aufgaben 4.1 bis 4.6) im Skript.
- Alle Aufgaben sind auf dem Papier zu lösen.
- Beachte: Bei Aufgabe 4.6 ist eine Konstruktionsbeschreibung gefordert (und nicht nur das Ausführen der auf Wikipedia beschriebenen Konstruktion).
- Erstelle eine kleine Zeichnung auf GeoGebra und finde heraus (Ausprobieren, Klassenkameraden fragen etc.), wie du sie als ggb-Datei auf deinem Rechner abspeichern und wieder laden kannst (nach einem Neustart von GeoGebra). Ich denke, dass es per “Herunterladen als …” geht. Wenn das mit dem Abspeichern gar nicht klappt, bitte ich um Mitteilung.
- Mindestens eine der Konstruktionen in Aufgabe 4.5 und 4.6 ist mit GeoGebra zu erstellen. Färbe jeweils die Objekte rot, die am Anfang der Konstruktion gegeben sind. Färbe das Fünfeck (= das Ziel der Konstruktion) blau (bis auf eventuell bereits rote Teile). Wenn man die roten Objekte verändert, müssen sich die blauen entsprechend mitverändern.2)
Abgabe
Schicke mir bis zum 5.12. (1aLIM) bzw. 6.12. (1rG) abends per Email deine GeoGebra-Datei zu Aufgabe 4.5 oder 4.6. Du darfst die Email ohne Anrede, Text und Gruss verschicken. Der Name der Datei muss wie folgt aussehen (der Betreff ist egal):
vorname-name-fuenfeck.ggb
(Eventuell steht hier bald eine einfachere Form der Einreichung, Sharepoint o.ä., aber ich weiss noch nicht, was da sinnvoll ist.)
Wichtig: Wer die GeoGebra-Sachen nicht selbst erstellen mag oder aus anderen Gründen keine Zeit dafür hat, schickt mir bitte nichts - Dateien kopieren kann ich selbst.
Jeder von Euch trägt selbst die Verantwortung für seinen/ihren Lernerfolg! Mein Job ist im Wesentlichen, für sinnvolle Materialien, Rahmenbedingungen und Erklärungen zu sorgen und bei Fragen zur Verfügung zu stehen.
Koordinatensystem (1rG am 2.12.2021; 1aLIM am 6.12.2021)
Abschnitt 4.3 lesen, Aufgabe 4.7 auf Papier bearbeiten. Wer Lust hat bzw. genügend schnell ist, darf sie natürlich auch per GeoGebra bearbeiten.
@1rG: Bitte sende mir wie oben beschrieben eine GeoGebra-Datei per Email (nicht per Teams). Wer diese Woche im Unterricht nicht bis Aufgabe 4.7 gekommen ist, holt dies bitte selbständig nach (Hausaufgabe). (Diejenigen, die krankheitsbedingt abwesend waren: Bitte mindestens bis Aufgabe 4.6 aufholen inklusive der GeoGebra-Datei!)
Motivation Geometrische Orte (1aLIM am 6. und 7.12.2021; 1rG am 7. und 8.12.2021)
Planimetrie bedeutet ebene Vermessung oder Ebenenvermessung, ähnlich wie Geometrie Erdvermessung bedeutet. Historisch gesehen ist es also sehr natürlich, “Landkartenprobleme” wie die folgenden zu betrachten:
Bearbeite das (doppelseitige) Arbeitsblatt Wanderer in der Wüste: 04-oasen-knobelaufgaben.pdf
Sinnvolle Ergänzung zur Wüsten-Aufgabe 3: Wo trifft die Trennlinie die Felsformation? Konstruiere diesen Punkt!
Geometrische Orte (1aLIM Start am 08.12.2021; 1rG Start am 09.12.2021)
Skript bis einschliesslich Kapitel 4.4 (samt Eintragungen): planimetrie-grundlagen-lv-seiten-1-bis-7.pdf
Zeittafel für 1aLIM:
- 07.12.2021: Wenige haben bereits mit 4.4.1 angefangen.
- 08.12.2021: Bis Aufgabe 4.8 einschliesslich (was bis dahin im Skript nicht während der Lektion erledigt wurde, ist Hausaufgabe)
- 13.12.2021: Bis Aufgabe 4.11 einschliesslich
- 14.12.2021: Merke-Boxen zu Parabel, Ellipse, Hyperbel ausgefüllt und erklärt (etwa, warum bei der Oase-Felsformation-Aufgabe eine Hyperbel herauskam bzw. genauer die Hälfte eines Hyperbelastes; Ellipse mit Gärtnerkonstruktion gezeichnet (Seil um zwei Pflöcke))
- Plan 03.01.2022: Die verbliebenen Aufgaben 4.12 bis 4.19 im Abschnitt 4.4.
- Plan 04.01.2022: Fragestunde vor der Prüfung
Zeittafel für 1rG:
- 09.12.2021: Bis Aufgabe 4.9 einschliesslich (was bis dahin im Skript nicht während der Lektion erledigt wurde, ist Hausaufgabe)
- 14.12.2021: Merke-Box zur Hyperbel ausgefüllt und erklärt (etwa, warum bei der Oase-Felsformation-Aufgabe eine Hyperbel herauskam bzw. genauer die Hälfte eines Hyperbelastes); wie findet man $d$, wenn die Hyperbel und die Brennpunkte gegeben sind?
- 15.12.2021: Merke-Box zu Parabel und Ellipse erklärt; Ellipse mit Gärtnerkonstruktion gezeichnet (Seil um zwei Pflöcke); kurz am Modell erklärt, warum Ellipse, Parabel und Hyperbel Kegelschnitte sind.
- 16.12.2021: Aufgaben 4.10, 4.11, 4.12, 4.17, 4.18 (Die Aufgaben 4.13 und 4.15 und 4.16 waren im Wesentlichen schon dran als Oasen-Aufgaben.)
- Plan 04.01.2022: Fragestunde vor der Prüfung, hoffentlich inklusive der noch fehlenden Aufgaben 4.14 (einfach für alle, die die Oasen-Aufgaben gemacht haben) und 4.19.
Bearbeite 4.1.
Bei 4.4.1 ist das erste Kästchen bereits vollständig ausgefüllt. Fülle die anderen Kästchen in ähnlicher Weise aus (zuerst mit Bleistift).
Hausaufgabe bis Anfang dritte Adventswoche (1aLIM und 1rG) (neben dem Vergleich deiner Lösungen während der Woche mit den unten auf dieser Seite veröffentlichten “Musterlösungen”):
Nimm dir für jede der beiden GeoGebra-Aufgaben mindestens 5 Minuten Zeit!
Falls das direkte Öffnen der GeoGebra-Dateien durch Anklicken nicht klappt: Speichere sie zuerst auf deinem Rechner. (Wenn du dann im Filemanager daraufklickst, klappt es vermutlich auch nicht direkt.) Starte GeoGebra und öffne die Datei von dort.
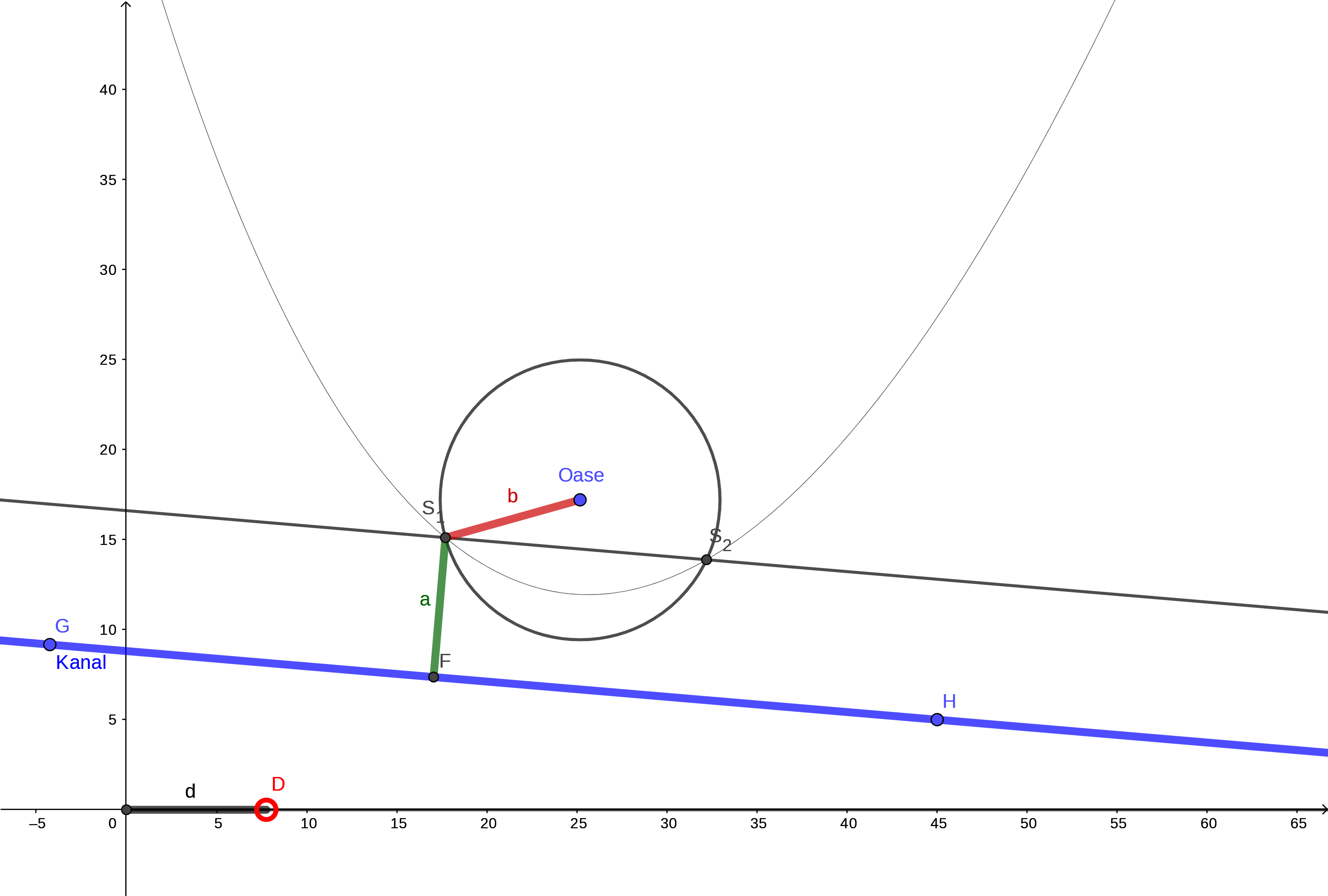
- Öffne die GeoGebra-Datei oase-kanal-parabel-bitte-mit-punkt-d-spielen.ggb und bewege den Schiebe-Regler-Punkt $D$ (und auch die drei blauen Punkte, wenn du magst). Falls nicht offensichtlich: Stelle den Zusammenhang zu deiner Lösung der Oase-Kanal-Aufgabe her.
- Die Kurve, auf der sich die beiden Punkte $S_1$ und $S_2$ bewegen, heisst Parabel. Der Scheitel der Parabel ist derjenige Punkt der Geraden, der am nächsten an der Kanal-Geraden liegt.
- Zoome weit heraus und weit hinein, um zu sehen, wie die Parabel “im Grossen” und “im Kleinen nahe ihres Scheitels” aussieht. Überzeuge dich insbesondere, dass die Parabel “keine Knicke” hat, sondern überall “glatt” und “gekrümmt” ist.
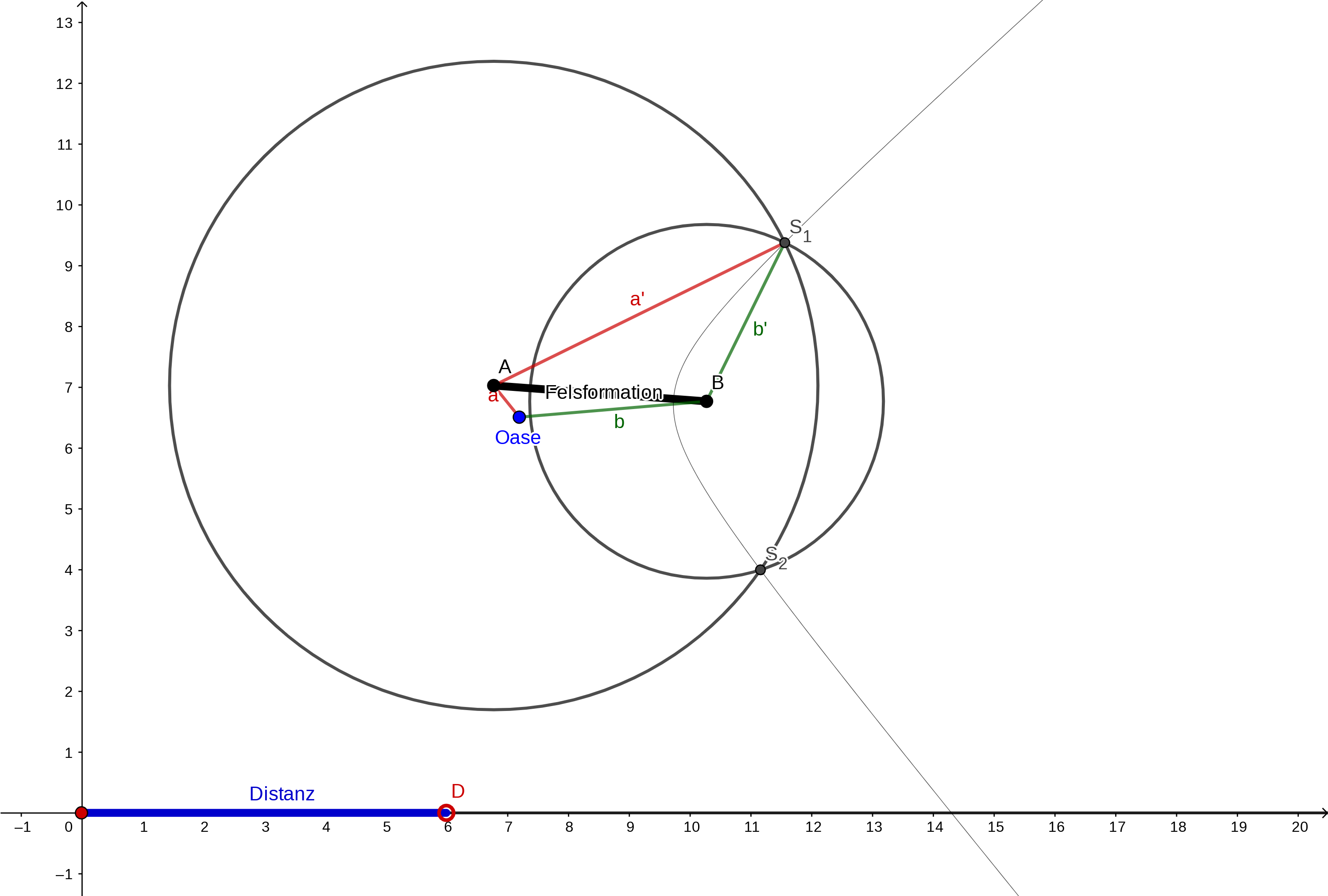
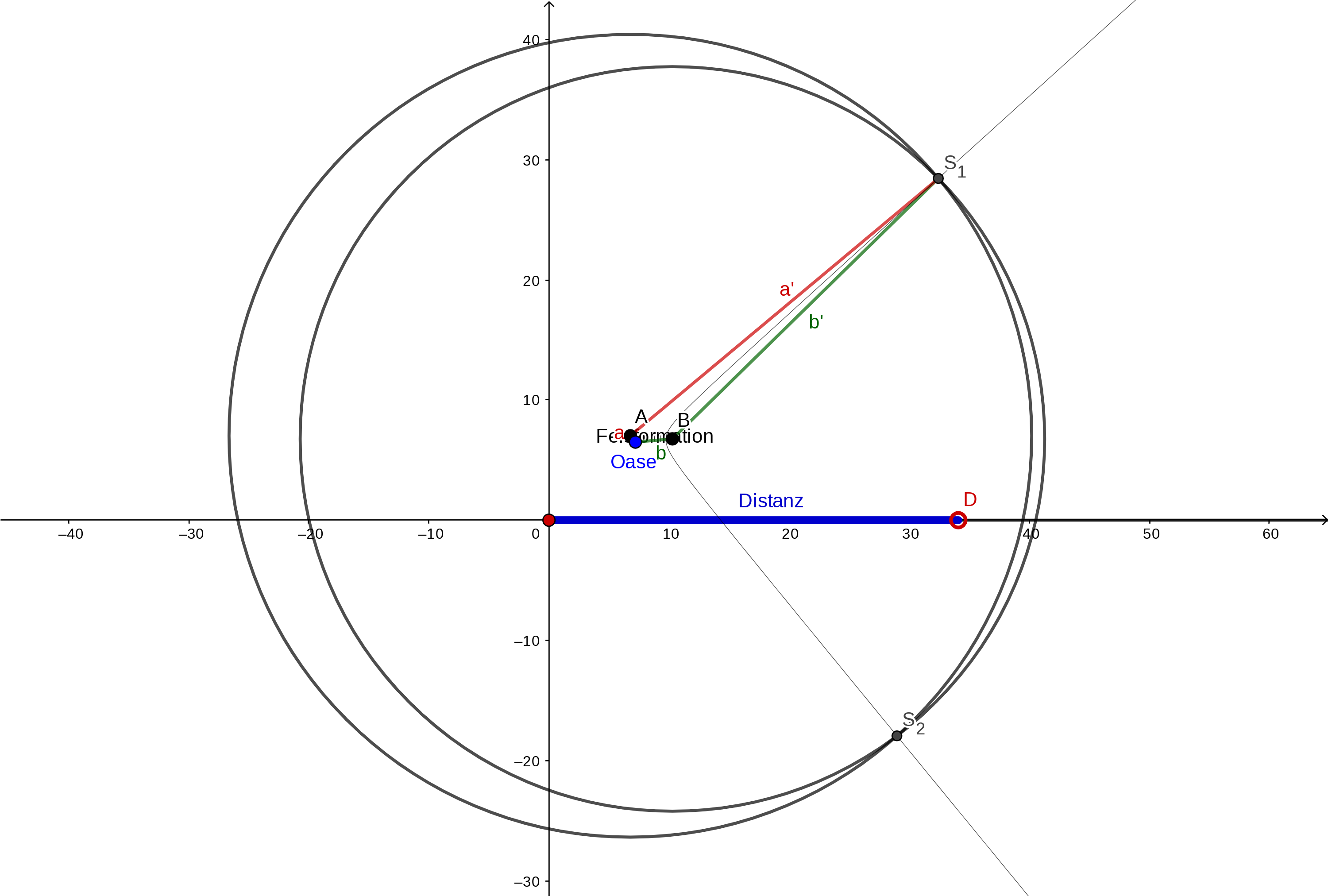
- Öffne die GeoGebra-Datei oase-felsformation-hyperbel-bitte-mit-punkt-d-spielen.ggb und bewege den Schiebe-Regler-Punkt $D$ (und auch die Punkte $A$, $B$ und den blauen Oasen-Punkt). Falls nicht offensichtlich: Stelle den Zusammenhang zu deiner Lösung der Oase-Felsformation-Aufgabe her. Was ist zusätzlich eingetragen?
- Die Kurve, auf der sich die beiden Punkte $S_1$ und $S_2$ bewegen, heisst Hyperbel (genau genommen handelt es sich nur um einen Ast der Hyperbel).
- Zoome weit heraus, um zu sehen, wie die Hyperbel “im Grossen” aussieht. Du wirst sehen bzw. vermuten, dass es zwei Geraden gibt, an die sich die Hyperbel immer besser anschmiegt, je weiter man “ins Unendliche” geht. Diese heissen Asymptoten (griechisch “nicht übereinstimmend” - aber ziemlich nah dran!). Wenn du ein Bild mit eingezeichneten Asymptoten sehen willst: Wikipedia: Hyperbel.
- Mittlerweile wohl klar: Überzeuge dich, dass die Hyperbel “keine Knicke” hat, sondern überall “glatt” und “gekrümmt” ist.
Lernen durch Lehren bzw. Wiederholen durch Erklären: Suche ein kritisches Familienmitglied oder eine:n Freund:in oder eine(n) Klassenkameraden/in mit etwas Zeit und Geduld, dem/der du mindestens eine der Aufgaben Oase-Kanal oder Oase-Felsformation mit Hilfe der obigen “GeoGebra Worksheets” erklärst.
Wenn du lieber klassisch arbeitest, darfst du es auch mit Zirkel und Lineal und Papier tun.
Freiwillig - auf dem Weg zum GeoGebra-Profi: Erstelle mit GeoGebra selbst ähnliche Dateien, wie ich sie oben zur Verfügung gestellt habe.
Hinweis: Der Icon “Ortslinie” hilft dir, alle Punkte zu markieren, auf denen sich gewisse Punkte bewegen – etwa hier die Schnittpunkte $S_1$ und $S_2$). Alternativ (und vielleicht leichter verständlich) kannst du die Punkte $S_1$ und $S_2$ mit der rechten Maustaste anklicken und dann “Spur anzeigen” wählen. Diese Spuren siehst du erst, wenn du einen deiner “Startpunkte” bewegst. Zum Beseitigen der Spuren von Punkten kurz Herein- und wieder Heraus-Zoomen.
Hilfen zu GeoGebra
Diverses, insbesondere einige Videos (etwa zum regulären Fünfeck), sind auf der Seite meines Kollegen Ivo Blöchliger zu finden: GeoGebra
Im Internet findet man natürlich sehr viele Erklärvideos und andere Materialien zu GeoGebra.
Einige Bemerkungen zum Abspeichern
(unter Windows - wir haben es aber auch auf dem iPad hinbekommen; ich schreibe als Linux-Benutzer auf, an was ich mich erinnere - keine Gewähr für Erfolg oder Korrektheit)
Zum Abspeichern auf der eigenen Festplatte (statt in irgendeienr Cloud) im rechten oberen Eck auf die drei waagerechten Linien klicken. Dort unter dem Menüpunkt “Datei” wähle man “Herunterladen als…” (und NICHT “Speichern”). Dort dann “Geogebra-Datei (.ggb)” als Dateiformat. Dann ändere man den Namen von “geogebra-export.ggb” zu dem gewünschten Namen, etwa “meine-konstruktion.ggb”, behalte dabei aber die Datei-Erweiterung “.ggb”. Dann klicke man auf “Speichern” und wählt nun noch genau aus, wo die Datei auf der Festplatte (o.ä.) gespeichert werden soll.
Wenn man dann GeoGebra schliesst, erscheint ein Fenster, dass man noch nicht alles gespeichert habe. Hier kann man unbesorgt auf “Nicht Speicher” klicken.
Wenn man die Datei wieder öffnen will, versucht man vermutlich, die Datei im Datei-Manager auszuwählen und anzuklicken. Dann startet zwar GeoGebra, jedoch wird die gewünschte Datei oft nicht geöffnet.
Stattdessen ist es besser, zuerst GeoGebra zu öffnen, dann ähnlich wie oben über die drei waagerechten Linien unter “Datei” den Menüpunkt “Öffnen” anklicken. Dann erscheinen links jede Menge bunte Bildchen, rechts unter dem GeoGebra-Symbol (eine Art Perlenkette) aber ein Ordner-Symbol. Dieses anklicken und dann die Datei suchen.
Wenn die Datei im Datei-Manager nicht als Symbol das GeoGebra-Symbol hat, ist sie vermutlich nicht korrekt als ggb-Datei abgespeichert und sollte umbenannt werden. Dies geht vermutlich direkt; alternativ klicke man mit der rechten Maustaste auf die Datei, gehe zu Eigenschaften und benenne die Datei um, etwa in “mein-name.ggb”.
(Wenn ich mich recht erinnere, ging das Datei-Öffnen beim iPad nicht so gut aus GeoGebra, aber dann irgendwie doch per Anklicken der Datei, wenn man dort vielleicht noch irgendwo eingestellt hatte, mit welcher Anwendung die Datei zu öffnen ist… Sorry und viel Erfolg.)
Einige Lösungen
- Lösungen bis Aufgabe 4.19 einschliesslich: loesungen-aufgaben-4.2-bis-4.19.pdf
- Lösung des Arbeitsblattes “Wanderer in der Wüste”: loesung-knobelaufgaben.pdf
Tipps beim Konstruieren mit GeoGebra
- (bemerkt bei den beiden Konstruktionen des regulären Fünfecks): Bewege die Ausgangsobjekte (meist Punkte) während der Konstruktionsphase. So siehst du hoffentlich schnell, wenn etwas schief läuft, du also etwa beim Auswählen eines Objekts ein (meist benachbartes) falsches Objekt ausgewählt hast.
- Beim Definieren eines Punktes ist es bisweilen “sicherer”, den Punkt als Schnittpunkt von zwei Objekten anzugeben als direkt den Schnittpunkt anzuklicken. Man kann oft die beiden sich schneidenden Objekte “weit draussen” anklicken (wo keine Verwechslungsgefahr besteht). Alternativ zoome man weit genug in die Zeichnung herein, um beim Auswählen Verwechslungen zu vermeiden. (Ctrl-Plus und Ctrl-Minus zum Zoomen oder per Maus, Bewegen des Zeichenblatts im Bewegemodus mit gedrückter Maustaste.
Wer von zu Hause aus dabei sein will
Da ich zur Zeit meist im Klassenzimmer herumgehe und Fragen beantworte, kommt mir die folgende Lösung vernünftig vor, falls jemand per Teams oder ähnlichem dabei sein will: Jemand von den Anwesenden ruft Euch per Teams an - so könnt ihr direkt mit dem- oder derjenigen kommunizieren und diskutieren. Wenn ich gebraucht werde, komme ich gerne dazu.
Im Skript sind an einigen Stellen “Bleistift-Icons”, wo etwas einzutragen ist. Ich versuche, davon stets Screenshots auf dieser Seite einzufügen.
Zur Prüfung in der ersten Woche nach den Weihnachtsferien
Eine Umfrage in der letzten Unterrichtswoche vor Weihnachten hat ergeben, dass von den Anwesenden niemand GeoGebra in der Prüfung verwenden will. Deswegen ist unten alles, was sich auf GeoGebra bezog, durchgestrichen. Falls jemand doch GeoGebra in der Prüfung verwenden möchte, möge man mir dies bitte schnellstmöglich mitteilen (vor Jahresende 2021).
In der Prüfung wird es
einerseitsAufgaben geben, die klassisch zu lösen sind (also auf Papier); hier kann auch Notation abgefragt werden (etwa $[AB$ oder $\overline{Pg}$ o.ä.) oder die Definition von Ellipse/Hyperbel/Parabel (in Worten oder mathematischen Symbolen)andererseits Aufgaben geben, die wahlweise klassisch oder mit GeoGebra bearbeiten werden dürfen. (Anteil vermutlich etwa ein Drittel).
Wer GeoGebra verwendet, muss mir seine Lösungen als GeoGebra-Dateien vor Ende der Prüfung per Email zusenden.
Vermutlich hat die Prüfung einen ersten Teil, der von den GeoGebra-Verwendern abgegeben werden muss, bevor ein Computer verwendet wird (etwa Abfrage von Notation oder Definitionen, was mit Computer und Internetzugang zu einfach wäre).
Stoff:
- Alles im Skript bis einschliesslich Abschnitt 4.4 “Geometrische Orte”.
- Alles auf dieser Internetseite (GeoGebra-Sachen optional).
- Optional: Grundkenntnisse der Software GeoGebra.
Lernziele
Sie kennen/wissen:
- Die Begriffe und Bezeichnungen der Planimetrie (Abschnitt 4.1 im Skript).
- Die Grundkonstruktionen mit Zirkel und Lineal (Abschnitt 4.2).
- Die Definition eines Koordinatensystems und wie Punkte in ein Koordinatensystem eingezeichnet werden.
- Die Begriffe und Bezeichnungen der geometrischen Orte der konstruktiven Geometrie (siehe 4.4.1).
- Die Definitionen von Parabel, Ellipse und Hyperbel als geometrische Orte und die zugehörigen Bezeichnungen (Brennpunkt(e), Leitlinie, Asymptote, Scheitel).
- Was Konstruktion mit Zirkel und Lineal bedeutet (also Konstruieren ohne Messen von Abständen und Winkeln)
Sie können:
- Konstruktionsbeschreibungen befolgen (vgl. Aufgaben im Abschnitt 4.2).
- Ordentliche Zeichnungen erstellen! (Sie sind selbst dafür verantwortlich, die nötigen Zeichenwerkzeuge Zirkel, Lineal in guter Qualität dabei zu haben.)
- Konstruktionsbeschreibungen aufschreiben (in Worten oder in der im Skript verwendeten Kurzform) (explizit wurden solche Beschreibungen im Abschnitt 4.2 verlangt; sehr viele Lösungen anderer Aufgaben im Skript enthalten Konstruktionsbeschreibungen).
- Punkte im Koordinatensystem einzeichnen und die Koordinaten (also $x$- und $y$-Koordinate) von Punkten ablesen.
- Geometrische Orte mit bestimmten Eigenschaften konstruieren bzw. skizzieren (vgl. alle Aufgaben im Abschnitt 4.4)
- Geometrie-Aufgaben von ähnlicher Schwierigkeit wie in den Abschnitten 4.1-4.4 im Skript lösen.
Man beachte, dass alle Konstruktionen, wie aus den Musterlösungen ersichtlich ist, in dem Sinne exakt sind, dass nirgendwo ein Punkt (etwa ein Mittelpunkt eines Kreises) oder ein Radius oder ähnliches “geschätzt”/“geraten” wird. “Geschätzte”/“geratene” Lösungen in der Prüfung geben keine Punkte. Wenn keine Konstruktionsbeschreibung verlangt ist, muss aus der Zeichnung ersichtlich sein, was gemacht wurde.