Polynom-Division
Erinnerung an schriftliche Division (mit Rest)
Lehrervortrag, Tafel oder eTafel
Erinnerung an schriftliche Division am Beispiel (wie oft passt 7 in …; multiplizere; subtrahiere; wie oft passt 7 in …. usw.)
- $95053 : 7$
Eine Variante dieses Verfahrens funktioniert auch für Polynome, wie du nun lernen wirst!
Warum ist das nützlich?
- Faktorzerlegung und
- Kürzen von Brüchen
Das lernen wir in der nächsten Woche.
Lernziel heute ist, das Verfahren “schriftliche Division von Polynomen” zu erlernen.
Aufgabe 1: Lernen am Beispiel, Schriftliche Division von Polynomen
Partnerarbeit (oder auch Einzelarbeit), ca. 10 Minuten; bei Fragen bitte melden
Versteht (im Sinne von “Rezept anwenden”) gemeinsam das Verfahren “schriftliche Division von Polynomen” mit Hilfe des hier verlinkten Beispiels.
Wer damit fertig ist, kann mit der nächsten Aufgabe weitermachen.
Aufgabe 2: Teste online, ob du das Verfahren verstanden hast
Einzelarbeit (gegenseitiges Helfen wie immer erlaubt), ca. 15 Minuten; bei Fragen bitte melden
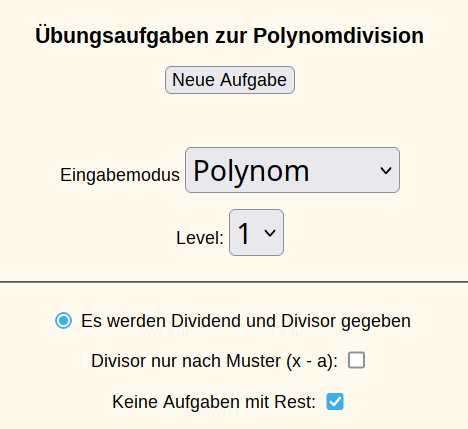
- Öffne in einem neuen Tab (neue Registerkarte) die Web-Seite http://www.arndt-bruenner.de/mathe/scripts/polynomdivisionueben.htm (vermutlich geht das automatisch, sonst
mouse right-clickoderCtrl+mouse left-click).
- Klicke auf den Button “Neue Aufgabe”.
- Löse solange Aufgaben auf Level 1, bis du 3 Aufgaben fehlerfrei gelöst hast und dich sicher fühlst.
Hinweise:
- Zur Eingabe von Potenzen am Computer: Schreibe
4x^3oder4*x^3für $4x^3$.
- Der Computer hilft dir, die Polynomdivision schrittweise durchzuführen und macht dich dabei sofort auf Fehler aufmerksam. Du sollst nicht die Division auf einem Blatt Papier durchführen und dann das Ergebnis eingeben.
- Wer Hilfe benötigt: Frag mich oder nutze die Hinweise im Fenster rechts oben.
Aufgabe 3: Mit Papier und Stift (oder Pen und Tablet), Vertiefung
Einzelarbeit, ca. 15 Minuten; bei Fragen bitte melden
- (a) Führe die folgende Polynom-Division mit Papier und Stift durch:
$$(x^2+9x-22):(x-2)$$
Bemerkung: Wenn du richtig gerechnet hast, bleibt kein Rest übrig.
- (b) Mache die Probe: Multipliziere dein Ergebnis mit $x-2$.
- (c) Führe die folgende Polynom-Division mit Papier und Stift durch:
$$(x^3+x^2-2x-8):(x-2)$$
- (d) Zeig mir deine Lösung! - Das erspart dir die Probe und ich sehe, dass du es verstanden hast.
- (e) Manchmal bleibt bei der Polynomdivision auch ein Rest übrig! Dividiere schriftlich
$$(x^2+9x-22):(x+2)$$
$\phantom{x}$
Bonus-Aufgabe
- (f) Überlege dir anhand deiner Rechnung bei Teilaufgabe (c), warum das Verfahren “funktioniert”! Erkläre es deinem Nachbarn.
Computerunterstütztes Üben (eventuell sinnvoll bei der Prüfungsvorbereitung)
- Du kannst neue Aufgaben (mit vorgegebenem Level) über den Link in Aufgabe 2 erzeugen und lösen, auch mit höherem Level und mit Rest.
- Deine Ergebnisse kannst du relativ schnell über den Link in Aufgabe 3 testen, falls du lieber mit Papier und Bleistift arbeitest (wie in der Prüfung).
- Auf http://www.arndt-bruenner.de/mathe/scripts/polynomdivision.htm#aufgaben kannst du auch direkt eine Liste von Aufgaben mit Lösungen (und Lösungsweg) erzeugen. Das Level ist aber relativ hoch.
Anwendungen der Polynomdivision: Faktorzerlegung von Polynomen und warum dies nützlich ist
Verfahren zur Faktorzerlegung; Erklärung am Beispiel
Betrachte das folgende Polynom, das nur ganzzahlige Koeffizienten (und Leitkoeffizient 1) hat. $$x^2-x\underbrace{-6}_{\text{konstanter Koeffizient}}$$
(1) Schreibe alle positiven UND NEGATIVEN Teiler des konstanten Koeffizienten auf:
$$1, 2, 3, 6, -1, -2, -3, -6$$
(2) Suche eine Nullstelle unter diesen Zahlen: (Eine Zahl heisst Nullstelle eines gegebenen Polynoms, wenn Null herauskommt, wenn wir $x$ durch diese Zahl ersetzen.)
- Ist 1 eine Nullstelle? Rechnung: $1^2-1-6 = -6 \not= 0$. Also ist 1 keine Nullstelle.
- Ist 2 eine Nullstelle? Rechnung: $2^2-2-6 = -4 \not= 0$. Also ist 2 keine Nullstelle.
- Ist 3 eine Nullstelle? Rechnung: $3^2-3-6=0$. Also ist 3 eine Nullstelle. Wir brechen die Nullstellensuche erfolgreich ab.
(3) Dividiere das Ausgangspolynom durch $x-(\text{Nullstelle})$, also in unserem Fall durch $x-3$. Polynomdivision liefert1)
$$(x^2-x-6):(x-3) = x+2$$
oder umgeschrieben
$$x^2-x-6 = (x-3) \cdot (x+2)$$
Dies ist die gesuchte Faktorzerlegung (oder Faktorisierung) unseres Polynoms.
Bemerkungen:
- Leicht sieht man, dass auch -2 eine Nullstelle unseres Polynoms ist. Hätten wir diese zuerst gefunden, hätten wir durch $x-(-2)$ dividiert und dieselbe Faktorisierung erhalten.
- Der konstante Koeffizient von $(x-3) \cdot (x+2)$ ist $(-3)\cdot 2=-6$ (denn die drei “anderen Produkte” enthalten $x$ mindestens einmal). Dies erklärt im Rückblick, warum wir die Liste der Teiler des konstanten Koeffizienten betrachtet haben.
Dieses Verfahren zur Faktorisierung von Polynomen mit ganzzahligen Koeffizienten funktioniert oft, aber nicht immer.
In unserem Beispiel hatte das Polynom Grad 2 (= die höchste auftretende Potenz von $x$). Das Verfahren geht genauso für Polynome von höherem Grad, nur muss man dann oft sehr viele Teiler darauf testen, ob sie Nullstelle sind.
Aufgabe 4, Faktorisieren quadratischer Polynome (= Polynome vom Grad zwei)
Wende das soeben erlernte Faktorisierungs-Rezept auf die folgenden Polynome an:
(Auch Raten ist erlaubt!)
- $x^2 -3x +2$
- $x^2 -7x +10$
- $x^2 + 3x + 2$
Manchmal ist eine Faktorzerlegung eines Polynoms auch aus anderen Gründen klar: Finde Faktorzerlegungen von (diese Faktorzerlegungen sind alle “offensichtlich”!)
- $x^2+3x$
- $x^2-6x+9$
- $x^2 - 4$
- $x^2 - 2$
Warum ist eine Faktorzerlegung eines Polynoms wie beispielsweise
$$x^2-5x+6 = (x-2) \cdot (x-3)$$
nützlich?
Antwort: Sie ist hilfreich für das
- Lösen von Gleichungen: Wenn man die Gleichung $x^2-5x+6=0$ lösen will2), so genügt es, die Gleichungen $x-2=0$ und $x-3=0$ zu lösen.
- Kürzen von Brüchen: Es gilt
$$\frac{x^2-5x+6}{x-3} = \frac{(x-2) \cdot (x-3)}{x-3} = \frac{x-2}{1} = x-2$$ 3) oder etwas komplizierter $$\frac{x^2-4}{x^2-5x+6} = \frac{(x-2) \cdot(x+2)}{(x-2) \cdot (x-3)} = \frac{x+2}{x-3}.$$
Aufgabe 5, "Zahnrad"-Icon, Faktorisieren eines Polynoms vom Grad 3
Schreibe das folgende Polynom dritten Grades als Produkt dreier Polynome ersten Grades! $$x^3-6x^2+11x-6$$