Table of Contents

Lektion 09

Ziele

Aufträge

Lösungen Intervalle

Lösungen Intervalle

Achtung: Es sind nicht alle Grössen normalverteilt, insb. Autopreise.

Die Intervalle berechnen sich jeweils aus Mittelwert $\pm$ $2\sigma$:

  • Geburtsgewichte: $[2024.9, 4499.4]$
  • Autopreise: $[-4731.3, 95521.4]$
  • Aktienrenditen: $[-0.02345, 0.02378]$

Theorie

Normalverteilung

Grosse Teile der Statistik beruhen auf der sogenannten Normaleverteilung. Eine Grösse resp. ein Merkmal ist normalverteilt, wenn die Ableitung der Verteilungsfunktion durch $f(x)=\frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}}$ gegeben ist. Für unsere Zwecke erscheint das aber kryptisch und wir beschränken uns darauf, festzuhalten, dass ein Histogram einer Standard-Normalverteilten Zufallsvariable wie folgt aussieht:

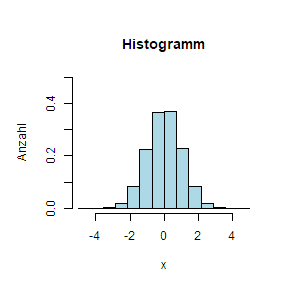
Aussehen Normalverteilung

Dabei ist wichtig festzuhalten, dass die Anzahl der Klassen in Histogramm offensichtlich willkürlich ist. Der theoretische Unterbau besagt aber, dass die Klassen beliebig klein gewählt werden können und das Histogramm zum Schluss (bei unendlich kleiner Klassenbreite und unendlich vielen Beobachtungen) dem Graphen der Funktion $f$ von oben entspricht.

Standardnormalverteilung und Standardisieren

Um nun sicher zu stellen, dass man immer von der gleichen Normalverteilung spricht, transformiert man Merkmale. Wenn $\mu_X=\frac1n\sum_{i=1}^n x_i$ und $\sigma_X=\sqrt{\frac1{n-1}\sum_{i=1}^n(x_i-\mu_X)^2}$ ist, dann sagt man, dass das Merkmal $Z=\frac{X-\mu}{\sigma}$ das standardisierte Merkmal von $X$ ist. Man kann dann jede Beobachtung $x_i$ zu $z_i=\frac{x_i-\mu}{\sigma}$ standardisieren.

$x_i$$x_i-\mu_X$$\frac{x_i-\mu_X}{\sigma_X}$
-5-9-1.21
510.13
510.13
0-4-0.54
15111.48
$\mu$400
$\sigma$7.417.411

Berechnet man nun den Mittelwert von $Z$ (geschrieben: $\mu_Z$) und die Standardabweichung von $Z$ (geschrieben: $\sigma_Z$) so kommt – egal wie $X$ ursprünglich verteilt ist – heraus, dass $\mu_Z=0$ und $\sigma_Z=1$ ist.

Beweis

Beweis

Es gilt ja $\mu_z=\frac{1}{n}\sum_{i=1}^n z_i = \frac{1}{n}\sum_{i=1}^n (x_i-\mu_x) = \frac{1}{n}\sum_{i=1}^n x_i -n\cdot\frac1n \mu_x = \mu_x-\mu_x=0$.

Das gleiche Argument kann für $\sigma_Z$ geführt werden: Die Rechnung wird etwas garstiger, funktioniert aber genau gleich.

Ist nun ein Merkmal $X$ normalverteilt so ist das standardisierte Merkmal standardnormalverteilt, das heisst, es ist normalverteilt Standardabweichung $\sigma=1$ und Mittelwert $\mu=0$.

Wahrscheinlichkeiten

Für standard-normalverteilte Merkmale – und damit auch für normalverteilte Merkmale – können sehr starke Aussagen über die Verteilung gemacht werden. So gilt z.B., dass im Intervall $[\mu_X-\sigma_X,\mu_X+\sigma_X]$ $68\%$ der Daten liegen. Für andere Vielfachen gilt die Tabelle unten:

k Prozent in $[\mu_x-k\cdot\sigma_X,\mu_x+k\cdot\sigma_X]$
1 $68.3\%$
2 $95.4\%$
3 $99.7\%$
4 $\approx 100\%$

Hat ein normalverteiltes Merkmal zum Beispiel den Mittelwert $\mu_X=11.2$ und $\sigma_X=3.1$ dann liegen ca. $68\%$ der Daten im Intervall $[8.1,14.3]=[11.2-3.1,11.2+3.1]$, das heisst in einem Intervall der Breite $2\sigma$, zentriert um den Mittelwert, liegen ca. $68\%$ der Daten.

Relevanz

Der Begriff einer (Standard-)normalverteilten Variable ist sehr wichtig: Einerseits, weil theoretisch gezeigt werden dann, dass die Summe vieler gleichartiger und unabhängiger Zufälle immer normalverteilt ist und andererseits weil eben gerade die Eigenschaft dazu führt, dass viele Daten in der “Welt da draussen” normalverteilt sind.

Aus einer mathematischen Sicht gilt noch anzumerken, dass zum Teil auch der Logarithmus eines Merkmals normalverteilt sein kann. Dies ist dann der Fall, wenn davon auszugehen ist, dass das Merkmal das Produkt vieler gleichartigen und unabhängigen Zufällen ist.

Daten in R

Daten Einlesen
# Daten aus Clipboard
inputdata <- read.table(file("clipboard"), sep = "\t")
# Gibt ein Dataframe aus der Excel-Zwischenablage zurück, getrennt durch
# Tabulator (so trennt Excel)

# oder
inputdata <- readClipboard(file("clipboard"))
# Falls eine einzelne Spalte

# oder
inputdata <- read.csv2("filenname.csv")
# Trennung durch Semikolon, daher csv2
Daten Standardisieren
insp <- inputdata$V2
mu <- mean(insp)
sd <- sd(insp)
hist(insp)
hist((insp-mu)/sd)

Wer möchte, kann hist noch mit breaks kontrollieren, damit gleich viele Säulen gezeichnet werden. Möchten man die Histogramme untereinander anzeigen, kann mit par(mfrow=c(2,1)) als erste Zeile gestartet werden.

Lösung

Lösung 

inputdata <- read.table(file("clipboard"), sep = "\t")
head(inputdata)
insp <- inputdata$V1
mu <- mean(insp)
sd <- sd(insp)
par(mfrow = c(2, 1))
hist(insp, breaks = 40,freq=F,main="Original")
hist((insp - mu)/sd, breaks = 40,freq=F,main="Z-Score")
curve(dnorm,add=T,col="red",lwd=2)

Lektion 08

Ziele

Aufträge

Theorie

Bei der Regression geht es letztendlich darum, den Zusammenhang, der in der letzten Lektion mit der Korrelation beobachtet worden ist, genauer zu beschreiben.

Die Idee der Regression ist, die Summe der quadratischen Abstände einer Geraden zu den beobachteten Datenpunkten zu minimieren. Dabei ist wichtig zu beachten, dass nur die vertikalen Abstände betrachtet werden:

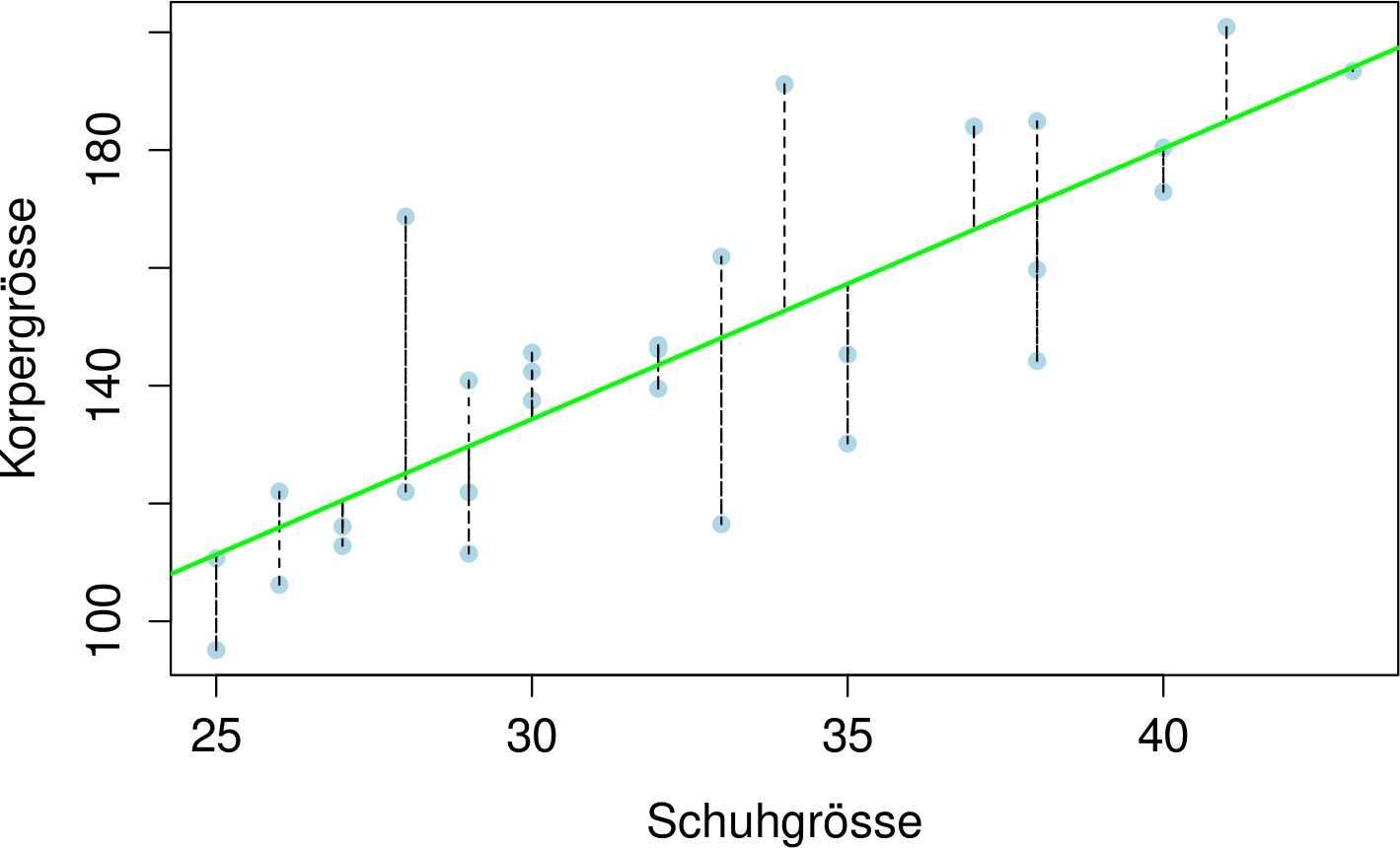
Jede lineare Funktion $g$ kann als $g:y=mx+q$ beschrieben werden. Man sucht also $m$ und $q$ so, dass die quadrierte Summe der Längen der gestrichelten Linien minimal ist.

Streng mathematisch ausgedrückt hat man die Wertepaare $(x_1,y_1),\, (x_1,y_1),\,(x_3,y_3), \ldots,(x_n,y_n)$. Hat man nun einen beobachtete $x$-Wert $x_i$ so ist die Vorhersage der Gerade für den $y$-Wert $mx_i+q$. Für ein gegebenes $m$ und $q$ ist damit der Abstand des $i$-ten Datenpunktes also $y_i-(mx_i+q)$, entsprechend ist der quadrierte Abstand des $i$-ten Datenpunktes $y_i-(mx_i+q))^2$.

Schliesslich sucht man eben $m$ und $q$ so, dass die Summe $$ (y_1-(mx_1+q))^2+(y_2-(mx_2+q))^2+(y_3-(mx_3+q))^2+\cdots (y_n-(mx_n+q))^2=\sum_{i=1}^n (y_i-(mx_i+q))^2 $$ minimal ist, das heisst, dass die Summe der quadrierten Abstände möglichst klein ist.

Betrachtet man diese Summe genauer, stellt man fest, dass dieser Ausdruck ein quadratischer Ausdruck ist, wenn man $m$ und $q$ als Variablen betrachtet. In anderen Worten, würde man – für gegebene Datenpunkte werden $x_i$ und $y_i$ zu Zahlen – diesen Ausdruck als Graph darstellen, erhielte man eine Parabel. Für Parabeln kann der Scheitelpunkt, welcher das Minimum der Parabel ist, einfach mit der Scheitelpunktformel berechnet werden.

Mit dieser Feststellung kann dann $m= \frac{\sum\limits_{i=1}^n (x_i - \bar x)(y_i - \bar y)}{\sum\limits_{i=1}^n (x_i - \bar x)^2}$ und $q=\bar y-m\bar x$ berechnet werden. Die Berechnung von $m$ und $q$ mit diesen Formeln führt zum Ziel, ist aber umständlich. Alle vernünftigen Datenanalyse-Programme können sogenannte Regressionsanalysen – oder eben Ausgleichsgeraden – berechnen.

R Tipps

Im Beispiel haben wir ein Datensatz gehabt mit den Spalten x und y. Die Idee ist, dass wir die gleichen Daten aus unseren Autodaten erhalten: Möchte man ausschliesslich die Daten eines Modells, könnte man wie folgt vorgehen:

datenaufbereiten.r
setwd("C:/Users/Simon.Knaus/git/ffstat/")
cardata <- read.table("bmw_data.csv",header = T,sep=";")
head(cardata) # Erste Zeilen (6) anzeigen
unique(cardata$model)
unique(cardata$treibstoff)
 
# Nur die Modelle 'x1'
selected <- cardata$model=="x1" 
# wie schaut der Vektor aus?
head(selected)
# Wie viele sind's? sum zählt TRUE als 1, FALSE als 0
sum(selected)
 
# Daten auswählen, d.h. Zeilen auswählen
regdata <- cardata[selected,]

Lösungen

Click to display ⇲

Click to hide ⇱

Berechnet man für die normalen Preise (nicht $\log$) die Regressiongerade, erhält man:

  • x1: $y = -0.3029\cdot x+47132$
  • x3: $y = -0.2412\cdot x+52607$
  • x4: $y = -0.3317\cdot x+65518$
  • x5: $y = -0.35\cdot x+78561$
  • x6: $y = -0.3912\cdot x+82847$

Für den X1 «kostet» also ein gefahrener Kilometer ca. 30 Rp, für den X6 kostet dieser ca. 39 Rp

Lektion 07

Ziele

Auträge

Theorie

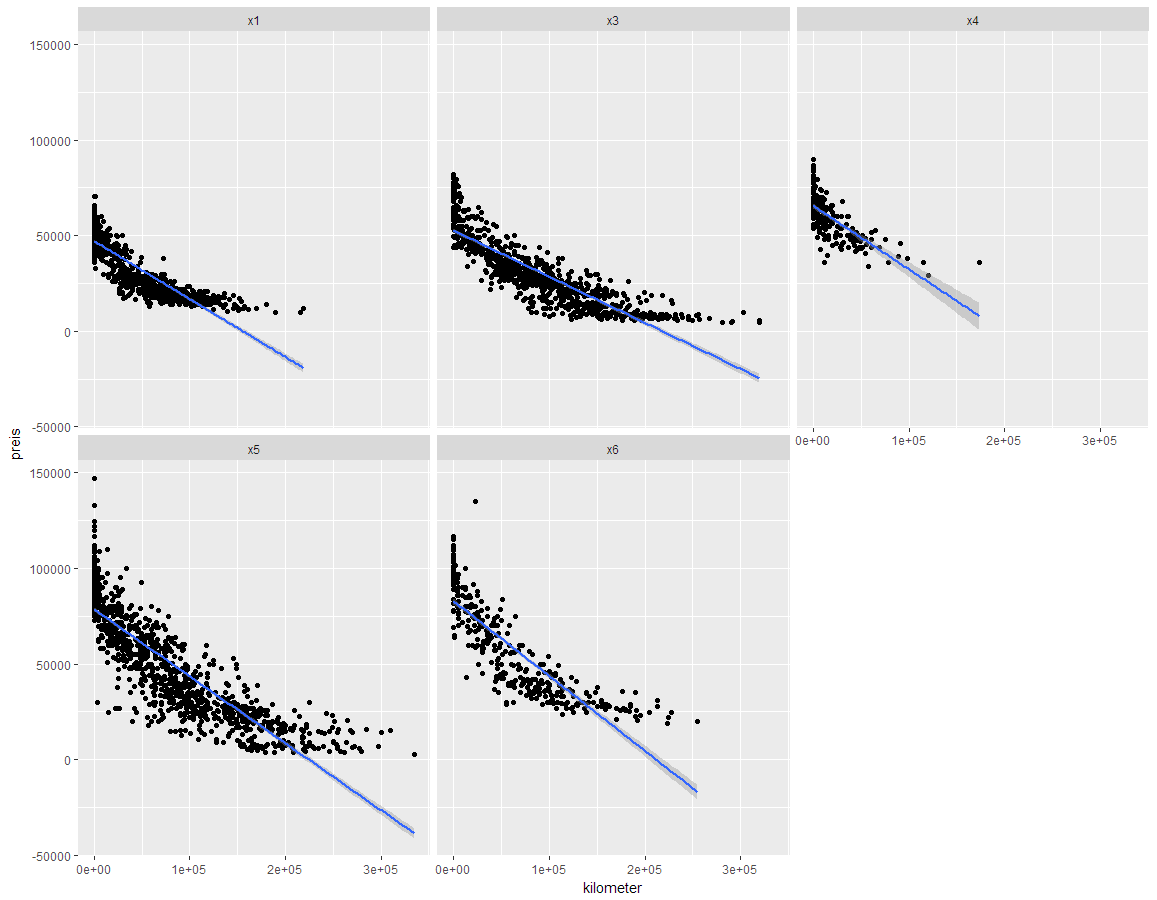
Wird ein Zusammenhang zwischen zwei kardinalen Merkmalen vermutet, sollte als erstes ein sogenannter Scatterplot erstellt werden. Zu diesem Zweck, wird das eine Merkmal auf der $x$-Achse und das andere Merkmal auf der $y$-Achse abgetragen.

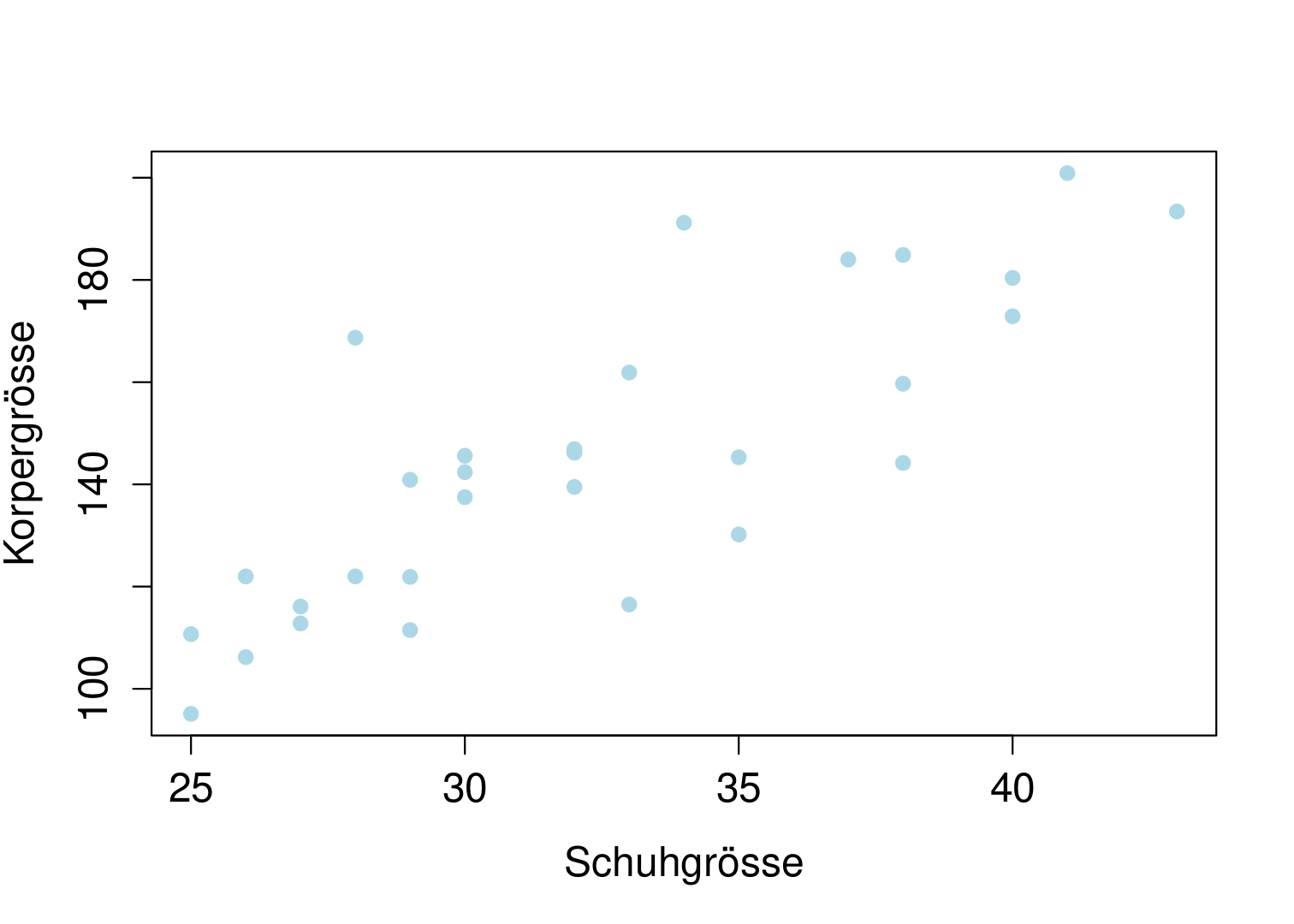
Nun gibt es ein Mass für diesen Zusammenhang: Die Stärke wie auch die Richtung des Zusammenhangs der Mermkale $X$ und $Y$, $R_{xy}$, wird mit der Korrelation gemessen: $$R_{xy}=\frac{\sum\limits_{i=1}^n (x_i-\bar{x})(y_i-\bar{y})}{\sqrt{\sum\limits_{i=1}^n (x_i-\bar{x})^2 \sum\limits_{i=1}^n (y_i-\bar{y})^2}}$$ Die Korrelation nimmt nur Werte zwischen $-1$ und $1$ an. In Excel wie auch in R sind Funktionen zur Berechnung der Korrelation hinterlegt. Wichtig dabei ist zu beachten, dass die Korrelation nur einen linearen Zusammenhang misst:

Möchte man die Stärke der Korrelation messen, quadriert man $R_{xy}$ zur $R^2=R_{xy}^2$. Man spricht von einem «starken Zusammenhang» wenn $0.5\leq R^2\leq 1$ ist, von einem «moderaten Zusammenhang» wenn $0.25\leq R^2 < 0.5$ ist, und schliesslich von einem «schwachen Zusammenhang» wenn $0.1\leq R^2<0.25$ ist. Ist schliesslich $R^2$ kleiner so liegt kein Zusammenhang vor. $R^2$ wird auch Bestimmtheismass genannt.

Zusammenfassend kann gesagt werden, dass Richtung und Stärke eines linearen Zusammenhangs gemessen werden kann:

Korrelation und Kausalität

Auch wenn $R^2$ sehr gross ist, muss das nicht heissen, dass in Tat und Wahrheit wirklich ein Zusammenhang dieser beiden Variablen vorliegt. Es kann durchaus sein, dass die Korrelation zufällig zu Stande gekommen ist. Man spricht dann auch von Scheinkorrelation oder in Englisch von spurious correlation.

Kausalität in diesem Zusammenhang besagt, dass ein Merkmal ein anderes bedingt: So ist zum Beispiel bei der Thematik Schuhgrösse und Körpergrösse wirklich davon auszugehen, dass ein kausaler Zusammenhang besteht.

Umsetzung in R

In R können Scatterplots mit plot erstellt werden:

plot.r
x <- c(2,3,7,10)
y <- c(7,1,2,30)
plot(x, y, main="Title")

Optional: Funktionen zeichnen

Optional: Funktionen zeichnen

Mit dem gleichen Befehl könnten auch Funktionen gezeichnet werden:

plot.r
x <- seq(-3,3, by = 0.1)
y <- x^2
plot(x, y, main="Parabel")
plot(x, y, main="Parabel",type="l")
plot(x, y, main="Parabel",type="h")

Die Korrelation kann mit cor berechnet werden:

plot.r
x <- c(2,3,7,10)
y <- c(7,1,2,30)
R <- cor(x,y)
R
R^2

Optional: Manuelle Umsetzung

Optional: Manuelle Umsetzung

In R werden Vektoren Element für Element multipliziert: Der Nenner könnte also wie folgt berechnet werden: 

 
x <- c(2,3,7,10)
y <- c(7,1,2,30)
x-mean(x)
(x-mean(x))*(y-mean(y))
sum((x-mean(x))*(y-mean(y)))

Korrelationen BMW Datensatz nach Modell

R-Code

R-Code 

library(corrplot)
png("C:/temp/corrbmw.png",width=300,height=1500)
par(mfrow=c(2,3))
for(mod in sort(unique(bmw$model))){
  tbmw = subset(bmw,model==mod)
  corbmw <- tbmw[,sapply(tbmw,is.numeric) & sapply(tbmw,function(inv){sd(inv,na.rm=T)>0})]
  corrplot(cor(corbmw,use="pairw"),main=mod,mar=c(0,0,1,0))  
}
dev.off()

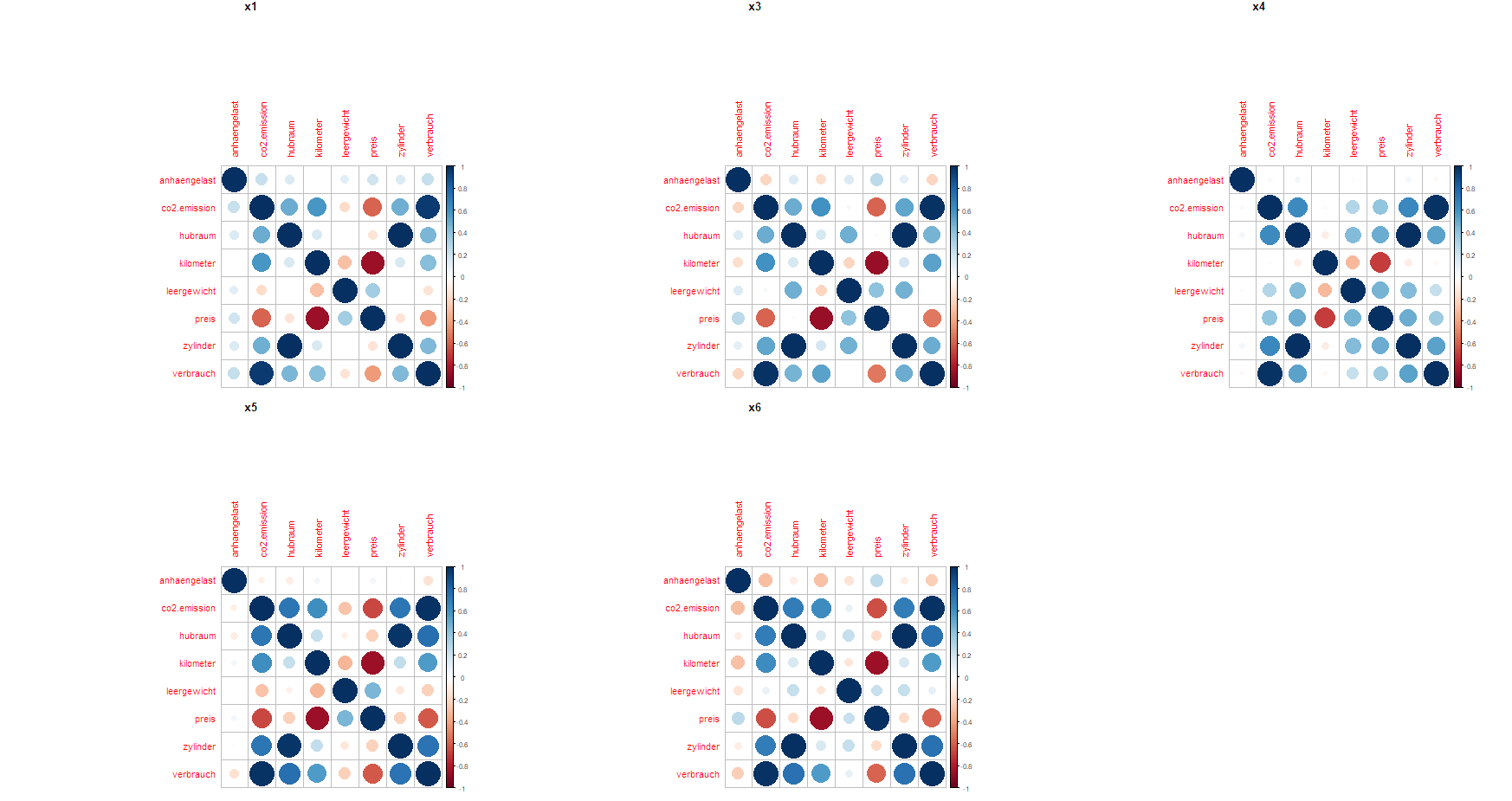
Lektion 06

Ziele

Aufträge

Theorie

Auf Grund der Lorenzkurve kann ausgesagt werden, wie stark die Merkmale (resp. deren Ausprägung) konzentriert sind (ein Konzentrationsmass). Das klassische Beispiel dabei ist die Einkommenverteilung. Die Frage, die dabei gestellt, resp. beantwortet wird, ist “Wie viel Prozent der Leute (Köpfe) verdienen wie viel Prozent des Gesamteinkommens?»

Einkommen Anzahl Personen Kumululierte relative Anzahl Einkommenssumme Kumululierte relative Einkommenssumme
2317 10 0.20 23'170 0.17
2552 11 0.42 28'072 0.37
2787 14 0.70 39'018 0.65
3022 8 0.86 24'176 0.83
3257 3 0.92 9'771 0.90
3492 4 1.00 13'968 1.00
Total 50 138'175

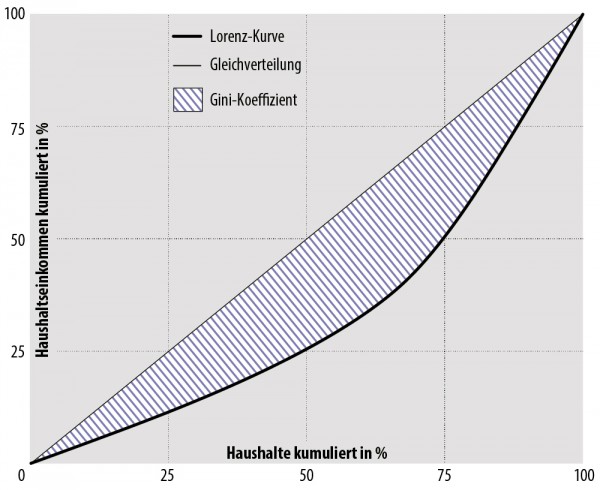
Zeichnet man nun die Punkte $(\text{Kumulierte relative Anzahl},\text{Kumulierte relative Einkommenssumme})=(x,y)$ und verbindet diese, erhält man die Lorenzkurve:

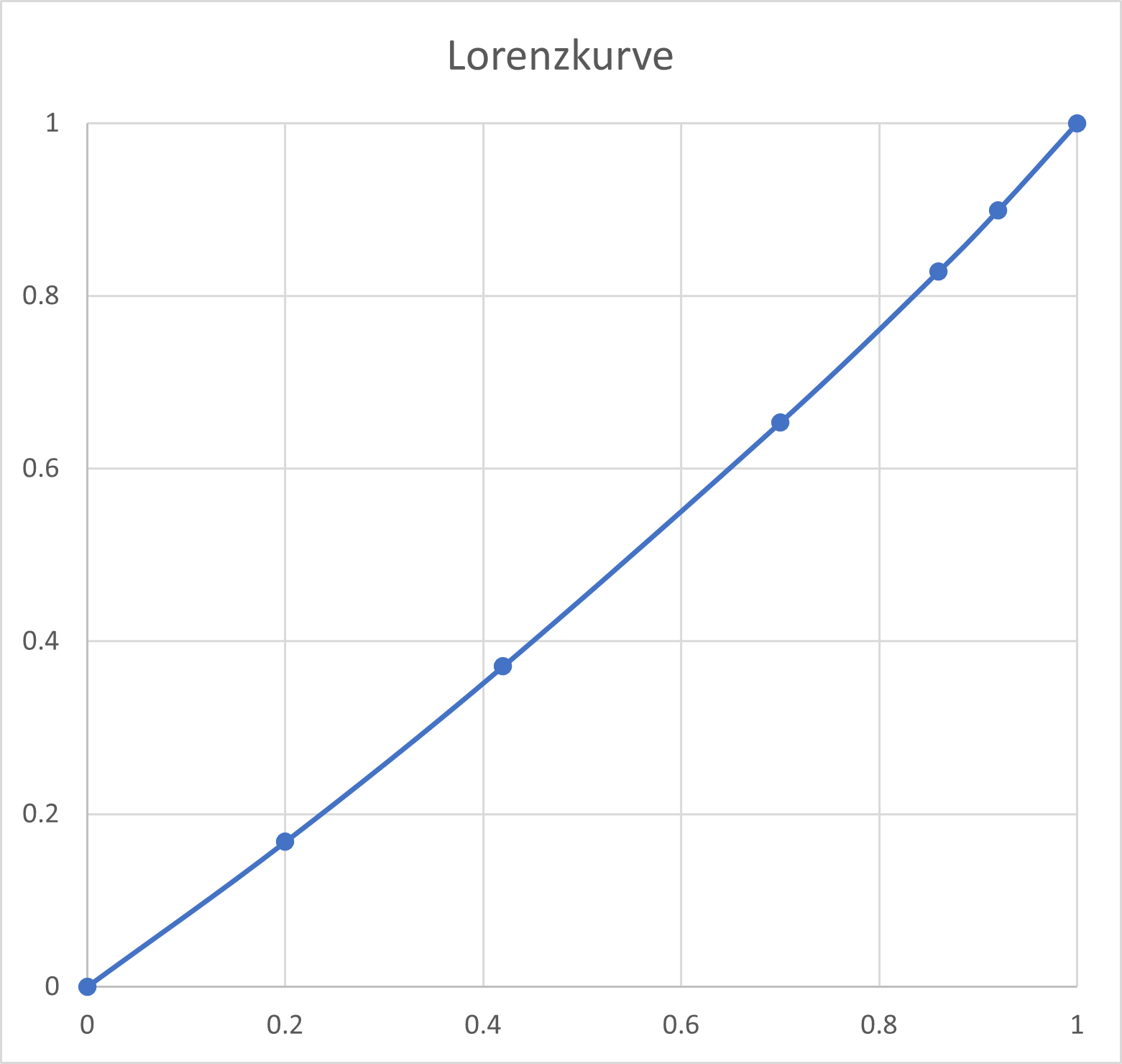
Zwischenfrage: Wo würden die Punkte liegen, wenn alle gleich viel verdienen würden?

Lösung

Lösung

Würden alle gleich viel verdienen, lägen die Punkte auf der Winkelhalbierenden.

Beispiele

Als Mass der Ungleichverteilung verwendet nun die Fläche, welche die Lorenzkurve mit der Winkelhalbierenden einschliesst. Diese Fläche nennt man auch Gini–Koeffizient

Gini-Koeffizient. Quelle: https://www.fuw.ch/wp-content/uploads/2015/01/

Als Beispiel für die Lorenzkurve wiederum die 5 BMW Modelle und ihre Preise. Achtung: Es handelt sich dabei nicht um ein Einkommen!

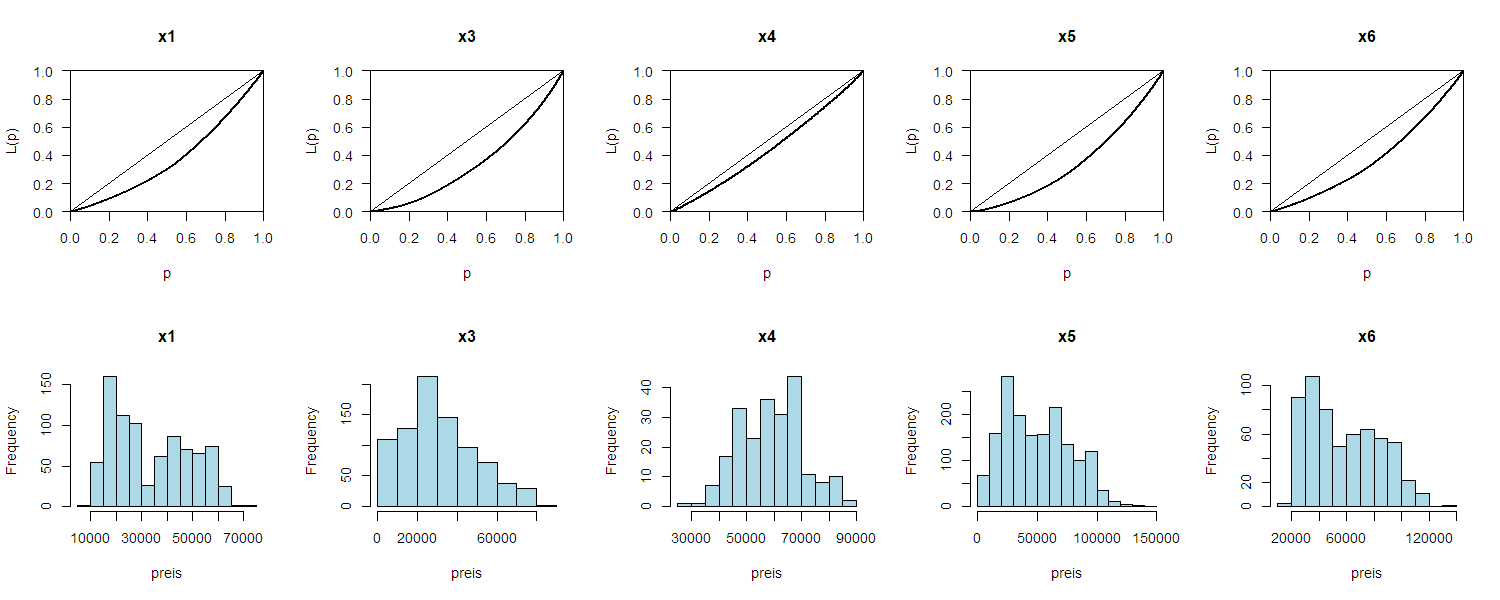
Die Lorenzkurve macht im Allgemeinen nur Sinn für Merkmale, mit positiven Werten (Preis, Einkommen, etc.)

Umsetzung in R

In R kann die Lorenzkurve ebenfalls umgesetzt werden. Wichtig sind dabei folgende Funktionen

Versuche mit den Funktionen oben, die richtigen $x$- und $y$-Werte zu erstellen und diese an anschliessend zu zeichnen.

Versuche zuerst mit «Dummy»-Date, dann kannst du dich um die Funktion kümmern, ohne die Daten einzulesen. 

dummydata <- c(70, 40, 70, 50, 30, 80, 90, 90, 40, 80, 40, 20, 40, 10, 
40, 60, 100, 30, 30, 70, 50, 70, 50, 40, 70, 60, 90, 50, 90)
xwerte <- ...
ywerte <- ...
 
plot(xwerte,ywerte)

Lösung als R Code

Lösung als R Code 

computeLorenzCurve <- function(x, plot = T) {
    nobs <- length(x)
    sortedx <- sort(x)
    abscissa <- (1:nobs)/nobs
    ordinate <- cumsum(sort(x))/sum(x)
 
    if (plot) {
        plot(ordinate, abscissa, main = "Lorenzkurve")
        abline(a = 0, b = 1)
    }
 
    return(cbind(abscissa, ordinate))
}

Lektion 05

Ziele

Aufträge

Boxplot

Ein Boxplot besteht aus einer Box, welche durch das erste und dritte Quartil ($Q_{25\%}$ und $Q_{75\%}$) begrenzt ist. Damit liegen $50\%$ der Daten in der Box. Der mittige Strich ist der Median ($q_{50\%}$), die Whiskers (Antennen oder Schnäuze) sind $w_1=Q_{50\%}-1.5\cdot IQA$ und $w_2=Q_{50\%}+1.5\cdot IQA$. $w_1$ und $w_2$ sind dabei zum Teil auch durch den grössten (resp. kleinsten für $w_1$) Wert eines Datenpunktes ersetzt, welcher gerade noch kleiner (resp. grösser für $w_1$) ist als $w_2$. Die Whiskers sind dann nicht symmetrisch. Die Punkte, die ausserhalb der Whiskers liegen, nennt man Outlier oder Ausreisser. Man kann zeigen, dass bei normalverteilten Daten, ca. $95\%$ der Beobachtungen innerhalb der beiden Whiskers zu liegen kommen.

# x1

# x3

# x4

# x5

# x6

Lösungen: Boxplot der Preise nach Modell

Click to display ⇲

Click to hide ⇱

Anwendungen Boxplot

Löhne in der Stadt Zürich

Lektion 04

Ziele

Auftrag

Lösung

Lösung

  • Mittelwert: -0.16
  • Modus: Nicht eindeutig.
  • Standardbweichung: 20.70
  • Varianz: 428.53
  • Median: 0.55
  • IQA: 33.3

Definitionen Lektion 04

Quantil

Ein Quantil gibt den dem Prozentrang zugehörigen Wert der Verteilung wieder. Der Median ist z.B. das 50% Quantil. Das 25%-Quantil z.B. ist der Wert, für welchen gilt, dass 25% der Werte kleiner und 75% der Werte grösser sind. Mathematisch kann man das wie folgt festhalten:

Möchte man das Quantil $\alpha=35\%=0.35$ von den $n=15$ Daten 10.6, 16.9, -27.3, 9.6, 18.1, -6.4, 34.4, 42.7, -3.6, 5, -3.2, 11.1, 46.1, 19.4, 2.4 berechnen, so muss man diese zuerst aufsteigend sortieren: -27.3, -6.4, -3.6, -3.2, 2.4, 5, 9.6, 10.6, 11.1, 16.9, 18.1, 19.4, 34.4, 42.7, 46.1. Die sortierten Werte werden mit $x_{(1)},x_{(2)},\ldots,x_{(n)}$ bezeichnet. Man sucht dann diesen Wert so, dass der gefundene Wert dem geforderten Prozentrang von $\alpha=0.35$ am nächsten kommt.

Genauer: Sei $K=\lfloor\alpha\cdot n\rfloor+1$ wobei $\lfloor\cdot\rfloor$ auf die nächste ganze Zahl abrundet. Für uns ist also $K=\lfloor0.35\cdot 15\rfloor+1=\lfloor5.25\rfloor+1=5+1=6$. Wir nehmen also den 6. Wert: Damit ist $Q_{0.35}=x_{(6)}=5$

Ist aber $\alpha\cdot n$ eine natürliche Zahl so, so nehmen wir wegen des Abrundens den mittleren der beiden Werte $x_{(K-1)}$ und $x_{(K)}$: Für $\alpha=0.3$ ist $K=3+1=4$ und damit $Q_{0.2}=\frac12((-3.6)+(-3.2))=-3.4$. $$Q_\alpha=\begin{cases}x_{(K)}\text{ wenn $\alpha\cdot n$ nicht ganzzahlig}\\\frac12\left(x_{(K)}+x_{(K-1)}\right)\text{ wenn $\alpha\cdot n$ ganzzahlig}\end{cases}$$

Quartile

Quartile sind die $25\%$, $50\%$ und $75\%$ Quantile einer Verteilung. Für das erste Quartil gilt also, dass $25\%$ der Beobachtungen kleiner sind, $75\%$ der Beobachtungen sind grösser.

Bei der Berechnung der Quantile kommen bei unterschiedlichen Softwarelösungen unterschiedliche Methoden zum Einsatz. Das heisst, u.U. stimmen die Quantile zweier unterschiedlichen Softwarelösungen nicht überein.

Interquartilsabstand (IQA)

Der Interquartilsabstand ist ein Mass für die Skala einer Verteilung. Wie weit sind das erste und dritte Quartil auseinander: $\text{IQA}=Q_{0.75}-Q_{0.25}$.

In Buch R-Reader:

R-Code

R-Code

cardata.r
# cardata <- read.table(readClipboard(),header = T,sep=';')
head(cardata)
unique(cardata$model)
x5 <- cardata$model == "x5"
x5  #ein Vektor mit TRUE and FALSE
x5preise <- cardata$preis[x5]
mean(x5preise)
median(x5preise)
sd(x5preise)
quantile(x5preise, 0.25)
quantile(x5preise, c(0.25, 0.75))
 
library(plyr)  # Zusatzpaket 'plyr' laden (vorgänig mit install.packages('plyr') installieren)
head(cardata)  # Erste Zeilen anzeigen
`?`(ddply  # Hilfe zu ddply
)
ddply(cardata, .(model), summarise, preis = mean(preis))  # Mittelwert des Preises nach Modell anzeigen
ddply(cardata, .(model), summarise, preis = median(preis))  # Median des Preises nach Modell anzeigen
ddply(cardata, .(model, zylinder), summarise, preis = mean(preis))  # Mittelwert des Preises nach Modell und Anzahl Zylinder anzeigen

Code für Modus

Code für Modus

mode.r
modes <- function(x) {
  uniquex <- unique(x)
  counts <- tabulate(match(x, ux))
  maxcount <- max(count)
  wheremaxcount <- maxcount==counts
  modevalues <- uniquex[wheremaxcount]
  return(modevalues)
}

Lektion 03

Ziele

Aufträge:

R Code Simulation Eile-mit-Weile

In R kann man auch Würfel (und vieles mehr) simulieren, mit sample wird eine Zahl aus einem Zahlenbereich zufällig ausgewählt. So könnte z.B. mit sample(1:45, 6, replace=FALSE) das Ziehen von 6 Zahlen beim Schweizer Zahlenlotto simuliert werden. 1:45 ist die Menge, aus welcher zufällig gezogen wird, 6 sind die Anzahl Elemente und replace=FALSE besagt, dass die Kugeln/Elemente nicht zurückgelegt werden vor dem nächsten Ziehen.

Mit replicate(n,{…}) wird alles n mal wiederholt, was zwischen den geschweiften Klammern steht.

Lösungen

Level 1

Lösung Level 1

Lösung Level 1

level1.r
sample(1:6, 1)
sample(1:6, 100, replace = TRUE)
sample(1:6, 1000, replace = TRUE)
 
res <- sample(1:6, 1000, replace = TRUE)
res == 6
sum(res == 6)  #Anzahl Sechsen
mean(res == 6)  #Durchschnittliche Anzahl Sechsen
Level 2

Lösung Level 2

Lösung Level 2

level2.r
sum(sample(1:6, 2, replace = T)) # zwei Würfel addieren
12 == sum(sample(1:6, 2, replace = T)) #vergleichen, ob gleich 12
replicate(1000, sum(sample(1:6, 2, replace = T)) == 12) #wiederholen 
mean(replicate(1000, sum(sample(1:6, 2, replace = T)) == 12)) #Mittelwert ausrechnen
Level 3

Lösung Level 3

Lösung Level 3

level3.R
rollDie <- function() {#erstellt Funktion, welche würfelt.
    isSix <- TRUE
    sum <- 0
    while (isSix) {
        thissample <- sample(6, 1)
        if (thissample + sum > 18) 
            break
        sum <- sum + thissample
        isSix <- thissample == 6
 
    }
    if (sum == 18) {
        sum <- 0
    }
    return(sum)
}
dice <- replicate(1e+06, rollDie())
hist(dice)
hist(dice, breaks = seq(-1, 17), main = "Histogramm Eile mit Weile", xlab = "Augenzahl", ylab = "Absolute Häufigkeit", col = "lightblue")

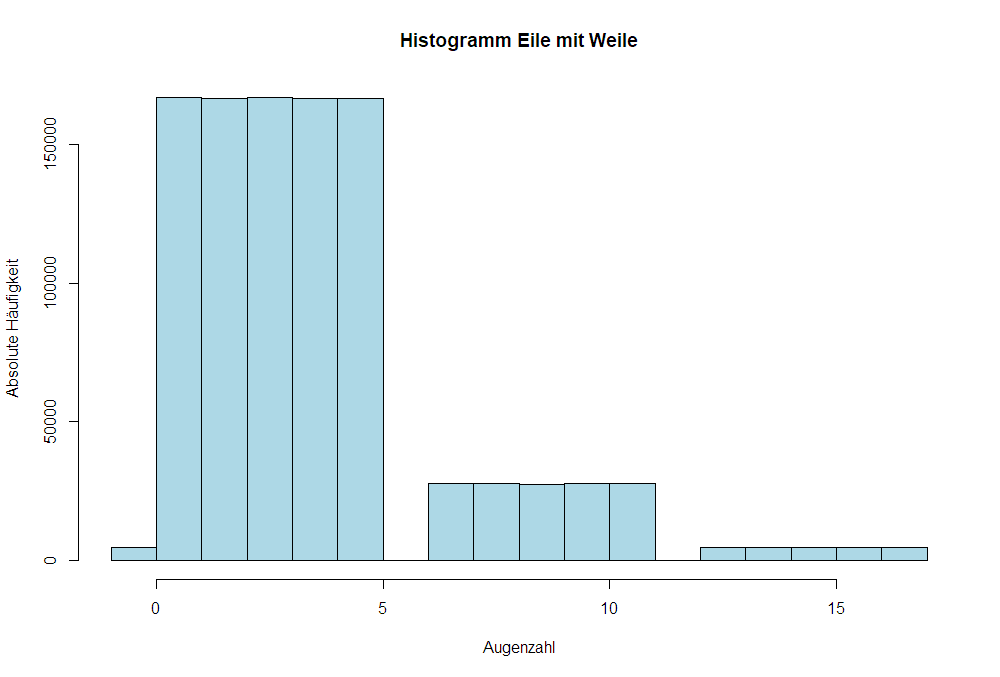
Histogramm Eile mit Weile bei 1'000'000 Würfeln

Lektion 02

Ziele

Aufträge

Einführungsvideos

Tip Abrunden

Tip Abrunden

Wenn man z.B. auf Fünf Rappen runden möchte: Man dividiert die Zahl durch 20, rundet die Zahl auf die nächste ganze Zahl (ab) und multipliziert dann wieder mit 20 ($100/5=20$)

Genauso kann man die gefahrenen Kilometer in “Buckets” einteilen: 

cardata$kilometerbucket <- 20000*floor(cardata$kilometer/20000)
ddplystattpivot.R
setwd("Pfad zum Arbeitsverzeichnis angeben")
cardata <- read.table("bmw_data.csv",header = T,sep=";")
 
# install.packages("plyr") # installiert Paket
 
library(plyr)
# Daten laden
cardata <- read.csv2("bmw_data.csv")
library(plyr) # Zusatzpaket 'plyr' laden (vorgänig mit install.packages("plyr") installieren)
head(cardata) # Erste Zeilen anzeigen
?ddply # Hilfe zu ddply
ddply(cardata, .(model), summarise, preis = mean(preis)) # Mittelwert des Preises nach Modell anzeigen
ddply(cardata, .(model), summarise, preis = median(preis)) # Median des Preises nach Modell anzeigen
ddply(cardata, .(model, zylinder), summarise, preis = mean(preis)) # Mittelwert des Preises nach Modell und Anzahl Zylinder anzeigen

Lektion 01

Ziele

Ziele der Lektion:

Auftrag

| intro.R
setwd("C:/Users/Simon.Knaus/git/ffstat") #Arbeitsverzeichnis bestimmen
cardata <- read.table("cardata.csv",sep=";",header=TRUE) #Daten einlesen als Dataframe
head(cardata) # Erste Zeilen (6) anzeigen
summary(cardata) # Zusammenfassung anzeigen
mean(cardata$preis) # Mittelwert des Preises anzeigen
unique(cardata$model) #Alle Modelle nur einzeln (einmalig) anzeigen
 
str(cardata) #Struktur des Dataframes anzeigen
cardata[2,1] #2 Zeile, erste Spalte
cardata[cardata$model=="x1", "preis"] #Model soll 'x1' sein, da die 'Preis'-Spalte
mean(cardata[2:4,2]) #Mittelwert der 2. bis 4. Zeile der 2. Spalte

Lösungen

Lösungen

solution01.R
#weisse autos suchen
weisseautos <- cardata$aussenfarbe=="weiss"
#preise von weissenautos
cardata$preis[weisseautos]
#mittelwert der preise
mean(cardata$preis[weisseautos])

#blaue autos suchen
blaueautos <- cardata$aussenfarbe=="blau"
#anzahl (länge) der blauen autos, resp. der Preise der blauen Autos
length(cardata$preis[blaueautos])
#auch möglich: Es ist TRUE 1; FALSE 0. Summe ist also alle TRUE
sum(blaueautos)

cardata[cardata$model=="x1", "preis"]
mean(cardata[cardata$model=="x1", "preis"])
mean(cardata[cardata$model=="x2", "preis"])
mean(cardata[cardata$model=="x3", "preis"])
mean(cardata[cardata$model=="x4", "preis"])
mean(cardata[cardata$model=="x5", "preis"])

Begriffe

Begriffe, die festzuhalten sind:

Begriff Kurzbeschrieb Excel R
Mittelwert Arithmetisches Mittel ($\mu$). Man schreibt auch $\bar x$. MITTELWERT() mean()
Anzahl Anzahl ANZAHL() length()
Merkmal Eigenschaften eines Datenpunkts (z.B. Türen, Farbe etc.)
Merkmalsausprägung und -typen Nominal (Farbe), Ordinal (Modell: X1 bis X6), Kardinal (z.B. Kilometer, Preis)
Absolute und relative Häufigkeit von $x$ Die absolute Häufigkeit entsprichen dem insgesamten Vorkommen, die relative Häufigkeit ist das Vorkommen in Prozent, d.h., die absolute Anzahl dividiert durch die Gesamtanzahl ANZAHL() oder SUMMEWENN()
Histogramm Illustration von Daten. Die Säulenfläche ist proportional zur relativen Häufigkeit
Varianz Die mittlere quadratische Abweichung, i.e. $\sigma^2=\frac1{n-1}\sum_{i=1}^n (x_i-\bar x)^2$ VARIANZA() var()
Standardabweichung Wurzel der mittleren quadratischen Abweichung $\sigma=\sqrt{\frac1{n-1}\sum_{i=1}^n (x_i-\bar x)^2}$ STABWA() sd()
Median Wert der mittig in der Verteilung aller sortierten Werte ist, resp. zum 50% Prozentrang gehöriger Wert MEDIAN() median()
Modus Der häufigste (die häufigsten) Wert(e)MODUS.EINF()Benutzerdefinierte Funktion modes(…)
$\alpha$-Quantil Zum Prozentrang $\alpha$ gehöriger Wert QUANTIL.INKL() quantile(,type=2)
IQA Interquartilsabstand. Differenz des 1. und 3. Quartils QUANTIL.INKL(…;.75)-QUANTIL.INKL(…;.25) IQR())